Crowdsourcing, Perfected.
Topcoder is a pioneer in crowdsourcing, with 20+ years of experience, and 325,000+ successful challenges in software development, data science/AI, UX design, and QA.
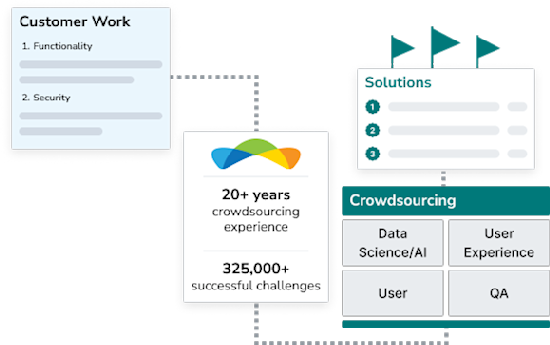
Crowdsourcing, Perfected.
Topcoder is a pioneer in crowdsourcing, with 20+ years of experience, and 325,000+ successful challenges in software development, data science/AI, UX design, and QA.









Revolutionize How You Get Work Done
Plug in Topcoder’s 1.9 million member global talent network to solve any technical problem.
Deliver your projects
Topcoder manages project delivery end-to-end, overseeing the global talent network to ensure quality.
Deliver your projects
Topcoder manages project delivery end-to-end, overseeing the global talent network to ensure quality.
Harness our expertise
The talent network has deep experience with software development, data science/AI, UX design, and QA.
Harness our expertise
The talent network has deep experience with software development, data science/AI, UX design, and QA.
Innovate complex work
Top talent competes to provide innovative solutions to your most complex problems.
Innovate complex work
Top talent competes to provide innovative solutions to your most complex problems.
Engage directly with freelancers
Discover expert freelancers and engage with them directly.
Engage directly with freelancers
Discover expert freelancers and engage with them directly.
Accelerate with AI
Our AI-powered platform helps you create requirements, match talent, and automatically review solutions.
Accelerate with AI
Our AI-powered platform helps you create requirements, match talent, and automatically review solutions.
Customers Love Us!
And Our Talent Is Awesome!
Achieve high-quality outcomes with
Topcoder.
Achieve high-quality outcomes with Topcoder.















