| | Consider a list of K unique integers given by {x1, x2, ..., xK }. This list is considered sorted in ascending order if x1 < x2 < ... < xK.
We define a plane as an N x N two-dimensional array of integers. A plane is sorted if each of the N rows (numbered from 0 to N-1) of the plane are a sorted list (as defined above) and each of the N columns (numbered from 0 to N-1) of the plane are a sorted list (as defined above).
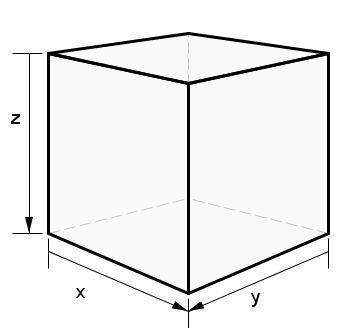
Finally, we define a cube as an N x N x N three-dimensional array of integers. In fact, such a cube consists of N planes (numbered from 0 to N-1). We can associate a Cartesian coordinate system with the cube as shown in the figure below. The arrows indicate the direction in which coordinates increase. Then, the 0th plane represents the top face of the cube (z = 0), and the N-1th plane represents the bottom face of the cube (z = N-1). A cube is sorted if each of the 3*N planes (i.e. all the planes with constant x, y, and z) in the cube are sorted (as defined above). An alternative definition is to say that if one point has all three coordinates less than or equal to another point, then the first point must have value less than or equal to the second point. In this problem, each integer from 1 to N3 inclusive will appear exactly once in the cube.
Create a class SortedCube with a single method sortCube. The method will take an int[] initCube as argument which gives the initial configuration of the cube, in plane-major order (that is, the first N*N numbers represent plane 0 of the cube, the following N*N numbers represent plane 1, etc.). Each plane is represented in row-major order (that is, the first N numbers represent row 0 of plane 0, the following N numbers represent row 1 of plane 0, etc.). In other words, the element with index N*N*Z + N*Y + X in the input is the value at coordinate (X,Y,Z).
In addition, you are given an int N. Your sortCube method should return a String[] array. Each element of the return array must be formatted as "X1,Y1,Z1-X2,Y2,Z2" (quotes for clarity only) where each of 'X1', 'Y1', 'Z1', 'X2', 'Y2', and 'Z2' represent an integer in the range 0 to N-1, inclusive. Each element describes two positions within the cube; specifically, (Xi, Yi, Zi) represents a position in the Zith plane, at (row, column) = (Yi, Xi). Thus, the array returned by your sortCube method describes the swaps that should be performed in the order they should be performed, so as to obtain a sorted cube.
Scoring
You will receive a score of 0 for a particular testcase if any of the following conditions are true for any element of the return array:
- (X1 < 0) or (X1 > N-1)
- (Y1 < 0) or (Y1 > N-1)
- (Z1 < 0) or (Z1 > N-1)
- (X2 < 0) or (X2 > N-1)
- (Y2 < 0) or (Y2 > N-1)
- (Z2 < 0) or (Z2 > N-1)
You will also receive a score of 0 if:
- The swaps described in your return array don't result in a sorted cube
- Any element of the return array is formatted incorrectly
- The returned array contains more than N3 elements
Otherwise, your score for a particular testcase will be N3/(numSwaps + 1), where numSwaps is the total number of elements in your returned array. The execution time limit is 30 seconds. Your total score will be the sum of your scores for each testcase.
Test Case Generation
Test cases are generated as follows:
|
