Problem Statement |
| | We have a sequence of numbers that we would like to sell to a number of
customers. We are concerned that some of our customers might resell this
sequence. While this is somewhat unavoidable, we'd like to be able to at
least trace any such sales back to their source: figure out who resold the
sequence.
Your task is to come up with a watermarking system that perturbs the sequence
slightly before giving it to a customer. Then, if we find an illicitly
obtained copy of the sequence, we can trace it back by reading the watermark.
If the sequence were resold unaltered, this would of course be trivial.
However, we want to make the watermarking robust enough that we can read it
even if the sequence is rather heavily distorted before being
resold.
A method watermark will be given a sequence of L doubles, along with an integer
N, and an integer C. You should return N watermarked copies of the sequence
of doubles, all concatenated into a single double[]. C will tell
you how much distortion your watermark must survive (see below). We will then
pick one of your watermarked sequences at random, distort it, and ask you to
identify it with a method identify. This method should return the 0-based
index of the sequence (i.e. 0 corresponds to the first L elements of your return, 1 to the next L and so on). The identify method will be called 100 times, with
sequences chosen and distorted independently each time.
The input sequence will be randomly generated with the following pseudocode:
d0 = 0;
d1 = 0;
d2 = 0;
d3 = 0;
for(int i = 0; i<L; i++)
d3 *= 0.99;
d2 *= 0.99;
d1 *= 0.99;
d0 *= 0.99;
d3 += gaussian()/1000;
d2 += d3;
d1 += d2;
d0 += d1;
seq[i] = d0;
To distort the sequence we will first chose a shift value from the Gaussian
distribution with standard deviation 10*C. The shift value will be added to
every value in the watermarked sequence. We will then add Gaussian noise with
mean 0 and standard deviation C to every value in the sequence. Some of the elements are then deleted, and finally a moving average of size C is applied. Full pseudocode for the sequence distortion follows:
perturb(seq)
shift = gaussian() * C * 10;
for(int i = 0 ;i<L; i++)
rr[i] = seq[i] + shift + gaussian() * C;
p = C/20.0;
skip = 0;
for(i = 0 ; i < L; i++)
p += gaussian() * 0.01;
if(p < 0)p = 0;
else if(p > C/10.0)p = C/10.0;
if(rand() < p)
skip++;
else
rr[i-skip] = rr[i];
for(i = 0; i<L - skip;i++)
avg += rr[i];
if(i >= C - 1)
ret[i - C + 1] = avg/C;
avg -= rr[i - C + 1];
return ret;
Your score for a single test case will be the total
squared error between your watermarked sequences and the original sequence, plus a penalty for incorrectly identified sequences. If your squared error is SE and you incorrectly identify W sequences, your test case score will be (SE+W)2W.
To compute your overall score, relative scoring will be used, where you
receive 1000*BEST/YOU point, where best is the lowest squared error.
You may download an offline tester also. |
| |
Definition |
| | | Class: | WatermarkSequence | | Method: | mark | | Parameters: | double[], int, int | | Returns: | double[] | | Method signature: | double[] mark(double[] seq, int N, int C) | | | | Method: | identify | | Parameters: | double[] | | Returns: | int | | Method signature: | int identify(double[] seq) | | (be sure your methods are public) |
|
| |
|
| |
Notes |
| - | There are 100 test cases. |
| - | Your class will only be instantiated once per test case, so you may save state between calls. |
| |
Constraints |
| - | You have 10 seconds to generate the marked sequence, and then 2 seconds per identification task (each timed independently). |
| - | The memory limit is 1024M. |
| - | The length of the original sequence will be between 1000 and 10,000, inclusive. |
| - | N will be between 2 and 100, inclusive. |
| - | C will be between 1 and 10, inclusive. |
| |
Examples |
| 0) | |
| | | Returns: "N = 54<br>
C = 4<br>
L = 1865<br>
" | The original sequence:
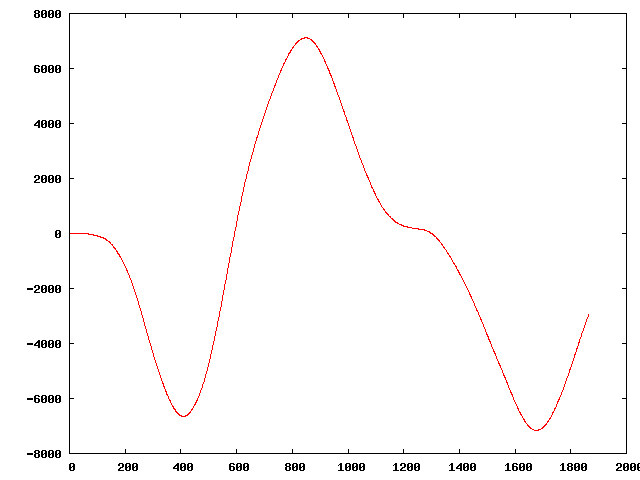
Three of the perturbed sequences (starting from the original):
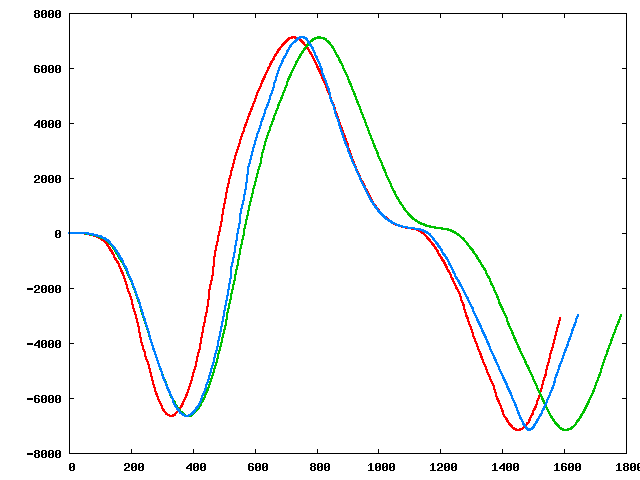
|
|
|
| 1) | |
| | | Returns: "N = 92<br>
C = 1<br>
L = 5636<br>
" | The original sequence:
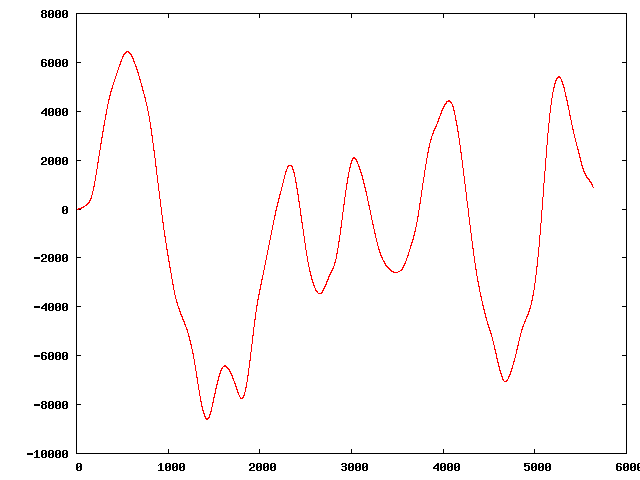
Three of the perturbed sequences (starting from the original):
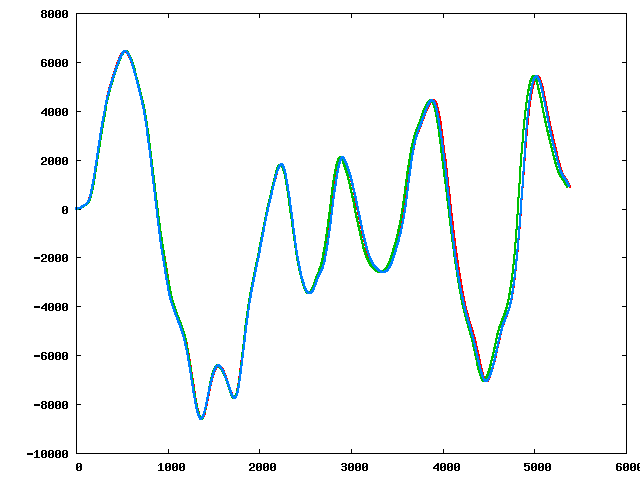
|
|
|
| 2) | |
| | | Returns: "N = 96<br>
C = 7<br>
L = 8494<br>
" | The original sequence:
Three of the perturbed sequences (starting from the original):
|
|
|
| 3) | |
| | | Returns: "N = 32<br>
C = 3<br>
L = 7141<br>
" | The original sequence:
Three of the perturbed sequences (starting from the original):
|
|
|
| 4) | |
| | | Returns: "N = 61<br>
C = 8<br>
L = 9201<br>
" | The original sequence:
Three of the perturbed sequences (starting from the original):
|
|
|
| 5) | |
| | | Returns: "N = 44<br>
C = 2<br>
L = 9085<br>
" | The original sequence:
Three of the perturbed sequences (starting from the original):
|
|
|
| 6) | |
| | | Returns: "N = 71<br>
C = 3<br>
L = 1947<br>
" | The original sequence:
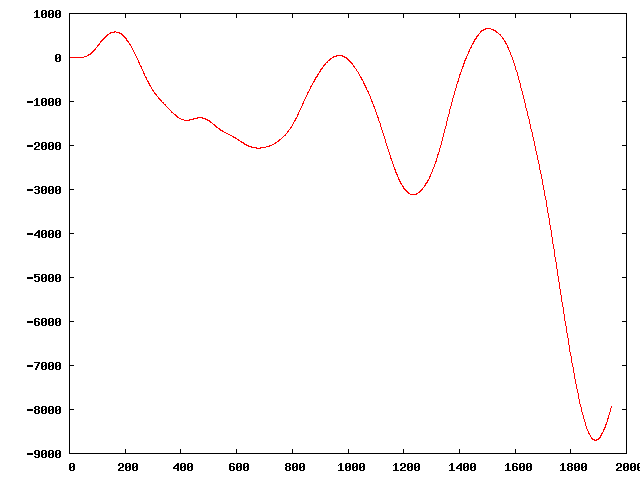
Three of the perturbed sequences (starting from the original):
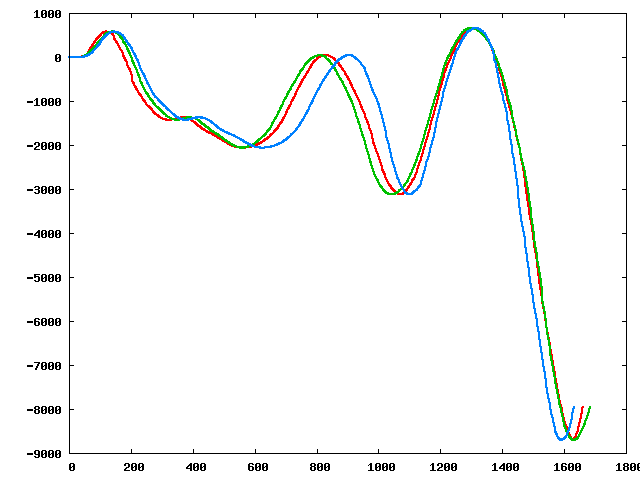
|
|
|
| 7) | |
| | | Returns: "N = 42<br>
C = 5<br>
L = 2805<br>
" | The original sequence:
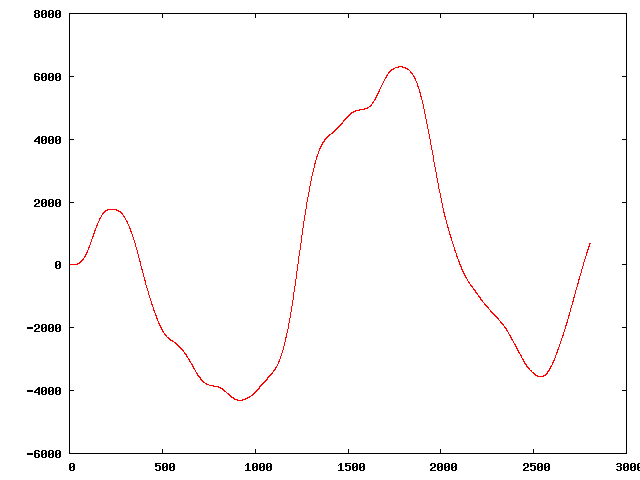
Three of the perturbed sequences (starting from the original):
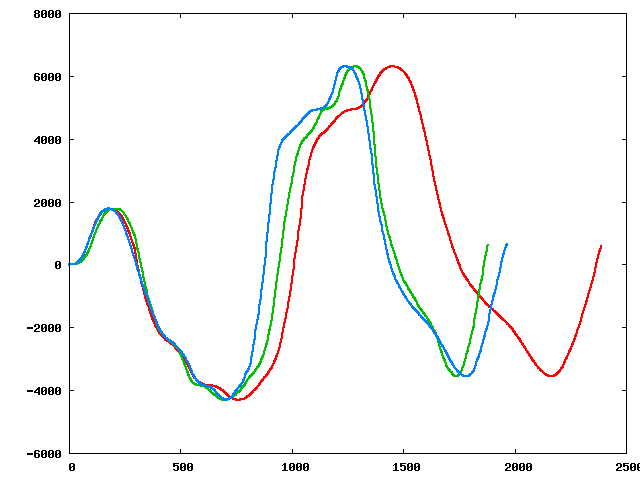
|
|
|
| 8) | |
| | | Returns: "N = 12<br>
C = 6<br>
L = 10045<br>
" | Note that none of the actual sequences will be this long, only this one example is over 10K. The original sequence:
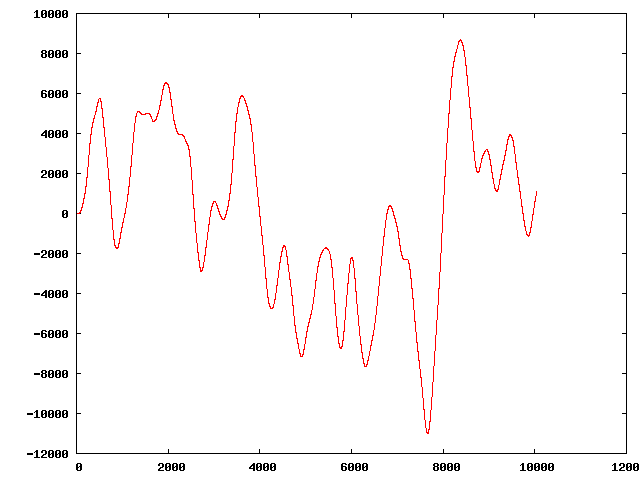
Three of the perturbed sequences (starting from the original):
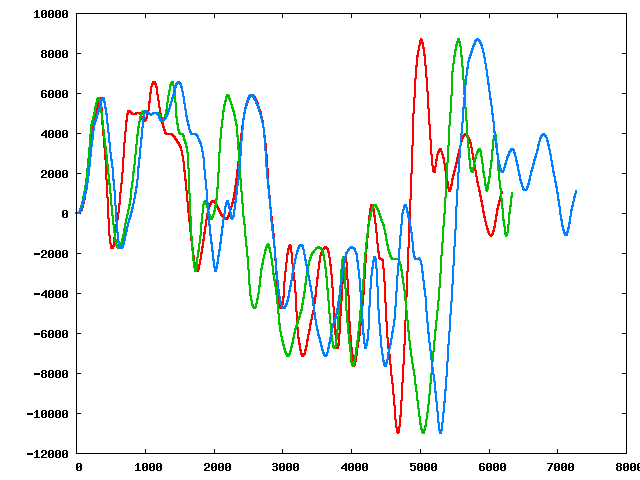
|
|
|
| 9) | |
| | | Returns: "N = 24<br>
C = 10<br>
L = 7098<br>
" | The original sequence:
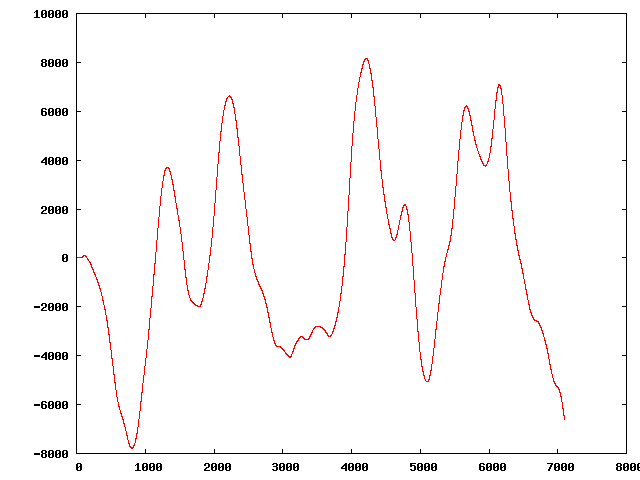
Three of the perturbed sequences (starting from the original):
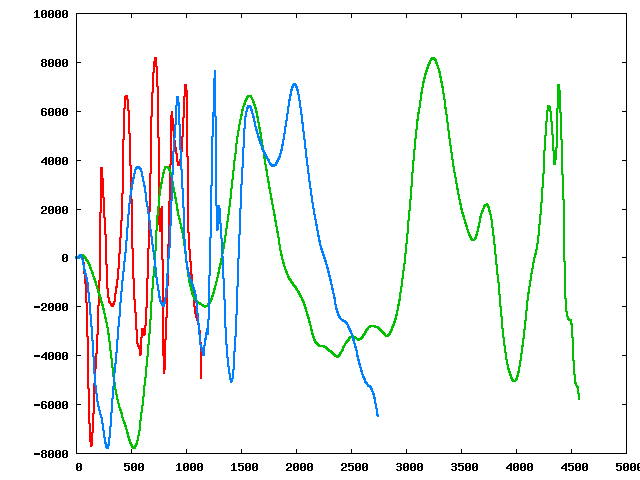
|
|
|
This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2020, TopCoder, Inc. All rights reserved.



















