Problem Statement

Automated Mechanical Failure Analysis Challenge

Prize Distribution

• 1st - $7,000
• 2nd - $3,500
• 3rd - $2,000
• 4th - $1,500
• 5th - $1,000
• Total - $15,000

Background

In the science of materials failure analysis, we are often interested in quantifying where a material has failed. To do so, we first employ a non-invasive 3D scanning tool that scans a volumetric sample looking for internal cracks. This procedure is similar to an MRI at the hospital. At each location in the sample, the scanner registers the probability of a crack being present. The output from this tool is a "crack probability cube" where each voxel contains a value from 0 to 255. A value of zero corresponds to a 0% probability of a crack being present and a value of 255 corresponds to a 100% probability of a crack being present at any given location. As the scanning technology is highly accurate, the population of probabilities is heavily skewed toward 0 or 255 with few intermediate values between. This cube of probabilities form the basis for our challenge dataset.

Cracks form to accommodate strain. They are discrete quantities that nucleate, grow, and terminate. Before we can understand the distribution of these discrete cracks, we desire to a apply a unique label to each individual crack that's present in the probability cube. Borrowing the MRI analogy again, this is the equivalent of looking at an MRI slice and identifying the end of one bone and the beginning of the next bone. Currently, this is a laborious procedure that's done by hand. We desire an algorithmic-based approach to expedite this process.

If we consider a single crack in isolation, it's trivially easy to apply a single label to an individual cloud of adjacent non-zero probabilities. The challenge arises when adjacent cracks intersect with one another. Seven heuristics are offered below to guide the labeling exercise in these ambiguous cases.

It's also worth noting that the shape of cracks are dictated by the confining stress fields in which they form. As gravity is always a factor in the net stress field, cracks tend to have a unique curvilinear expression when viewed top-down (i.e. Z-slices or Z-axis normal). Viewing from any other cardinal direction (i.e. from the west, east, south, or north) tends to yield a similar expression where the cracks appear more planar and straight. Human experts tend to prefer discretizing cracks using Z-slices to guide their efforts.

Labeling Heuristics for Ambiguous Cases

Ambiguity 1: parent-child relationship. Two cracks intersect and the blue crack occurred first. They also have clearly different orientations. They should be labeled separately.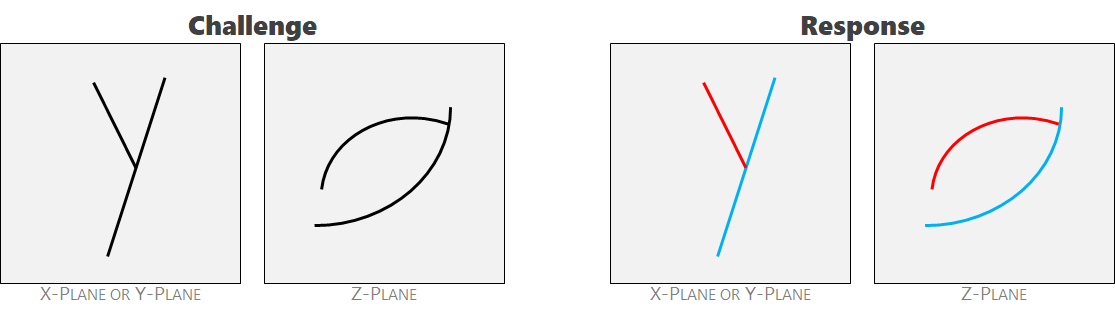

Ambiguity 2: generational offsetting. The red crack post-dates the blue crack and creates a gap in the blue. The two also have different orientations. They should be labeled separately.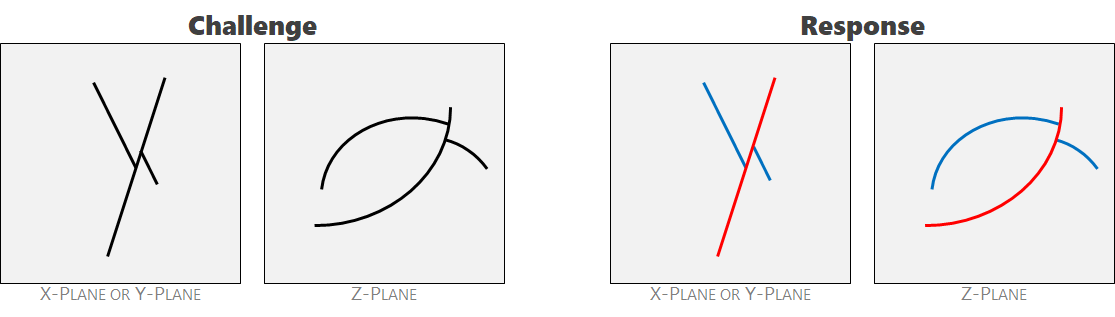

Ambiguity 3: mid-field aberrations. An aberration in the field is present or the crack magnitude fell below the detection limit of the tool. This is a measurement error. A human expert might infer a single crack to be through-going. These two features should be labeled as a single crack.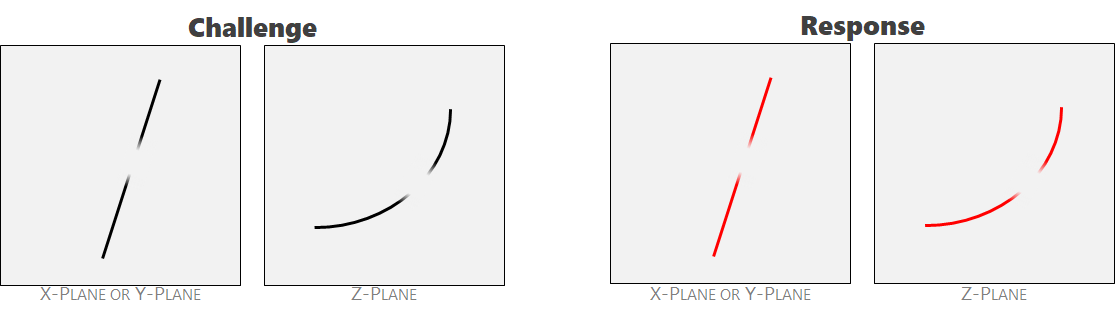

Ambiguity 4: split-ends. The crack feathers at the end. The feather-tip that most closely resembles the character of the main feature shares the same label. Note the similarity in orientation and curvature.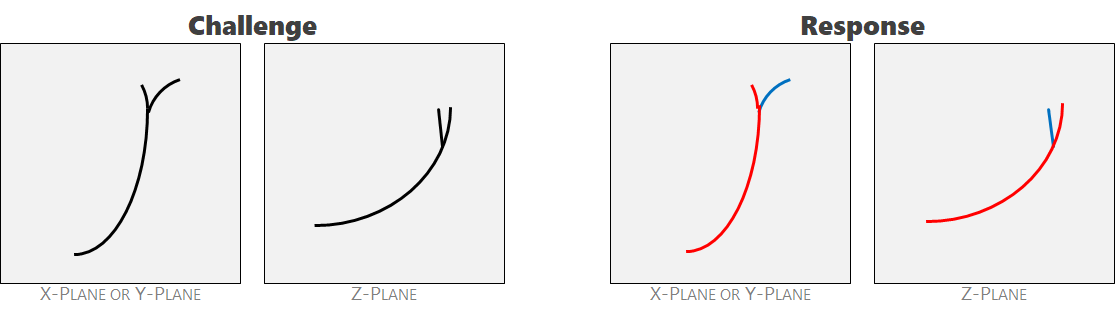

Ambiguity 5: acute angles. Cracks can't form acute angles. The two intersecting features receive separate labels.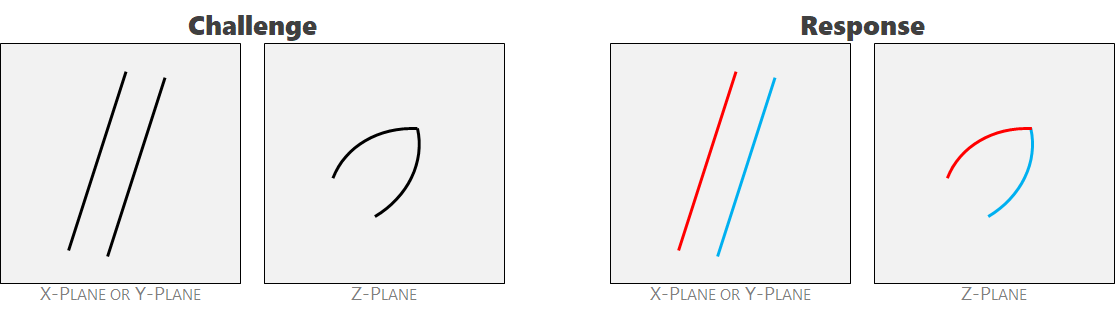

Ambiguity 6: birefringence. The imaging tool scans along the X-plane and then the Y-plane. The two results are then combined. Sometimes, a single crack registers in slightly different spaces. We call this phenomenon 'birefringence.' This outcome should receive a single label.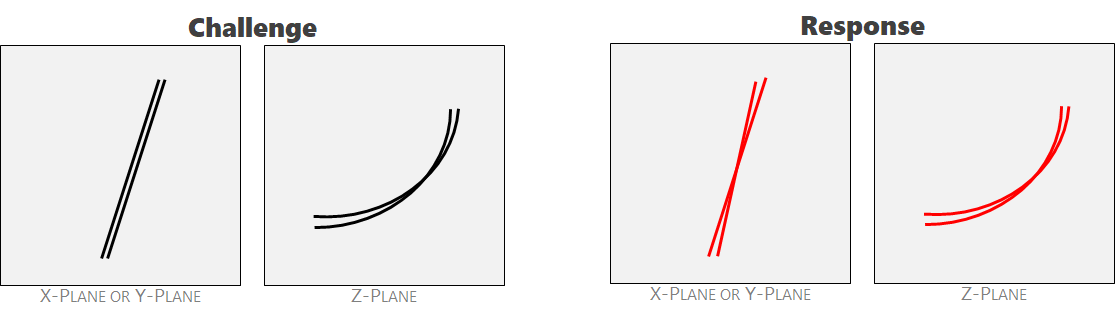

Ambiguity 7: de minimus bodies can be ignored. Cracks that are smaller than an arbitrary threshold may be ignored and not labeled. This threshold isn't exact, but is on the order of <10 voxels in height or width.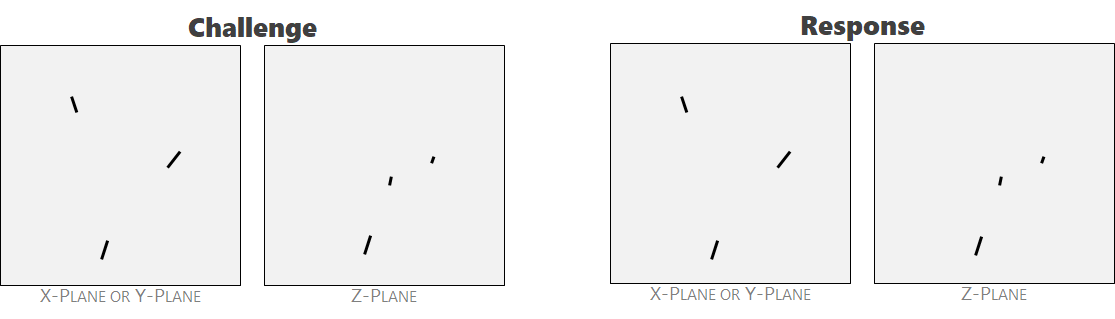

Objective

The objective of this challenge is to apply a label to each discrete crack that has been imaged in the crack probability volume challenge dataset. As a matter of convention, all non-zero probability values should receive a label between 1 and 1000. All zero-valued probabilities should receive a label of 0 (implying no crack present). While labels of 1 and 2 have special meaning in the input ground truth file, you are free to use these values in your labelling where they have no special significance.

Input Data Files

The input data set consists of a three dimensional array of integer values between 0 and 255, inclusive. The size of this three dimensional array is 333 (z) x 480 (y) x 640 (x) voxels (a total of 102,297,600 voxels). This 3D array is indexed in the order (z, y, x), i.e. there are 333 Z-slices. This 3D array is provided in the form of a python numpy array and of a run length encoded csv file. Both formats are within a zip file which can be downloaded here. In the run length encoded csv file, the voxel at (z, y, x) is indexed as follows (where z, y, x, and voxel index are all zero-based):

The run length encoded file contains two columns: value and count. Each row in this file represents a "run" of the same value, count times. For example, the row "255,4" represents the value 255 repeated 4 times: 255, 255, 255, 255. The decoded values will be in order of voxel index, and the (z, y, x) coordinates can be determined from the previous voxel indexing formula.

This three dimensional space has been partitioned into three regions for this contest:

• Training (0 ≤ x < 256) : Used for training with provided ground truth label file
• Provisional (256 ≤ x < 384) : Used for leaderboard scoring during the contest
• System (384 ≤ x < 640) : Used for final system scoring

The 3D array of ground truth labelling of the training region is provided in the form of a python numpy array and of a run length encoded csv file. Both formats are within a zip file which can be downloaded here. The run length encoded file has the same format as the previously described run length encoded probability file, except the values are the labels instead of the probabilities.

The provided ground truth labelling file only contains labels for certain Z-slices (z = 0, 18, 34, 51, 68, 84, 101, 118, 134, 151, 167, 184, 201, 218, 234, 250, 268, 284, 301, 318, 332). On all remaining non-labeled slices, all non-zero probability voxels have a label of 1. In labeled slices, voxels where the crack labelling is ambiguous have a label of 2. Voxels with a ground truth label of 1 or 2 are not scorable. Only voxels with ground truth labels greater than 2 will be used for scoring.

A visualizer tool has been developed in a previous series of challenges to view this three dimensional array. This tool is designed to work with the numpy 3D array file. This latest version of this tool can be downloaded here. Python 3.6.2+ is required in order to run the visualizer.

The required libraries can be installed with the following command:

or

The visualizer is then started with the following command:

The following image from the visualizer displays the ground truth labeling of a small portion of a single Z-slice. In this image, the bright green marks correspond to label 2, which means the crack is ambiguous. All other colors in this image correspond to unique crack labels.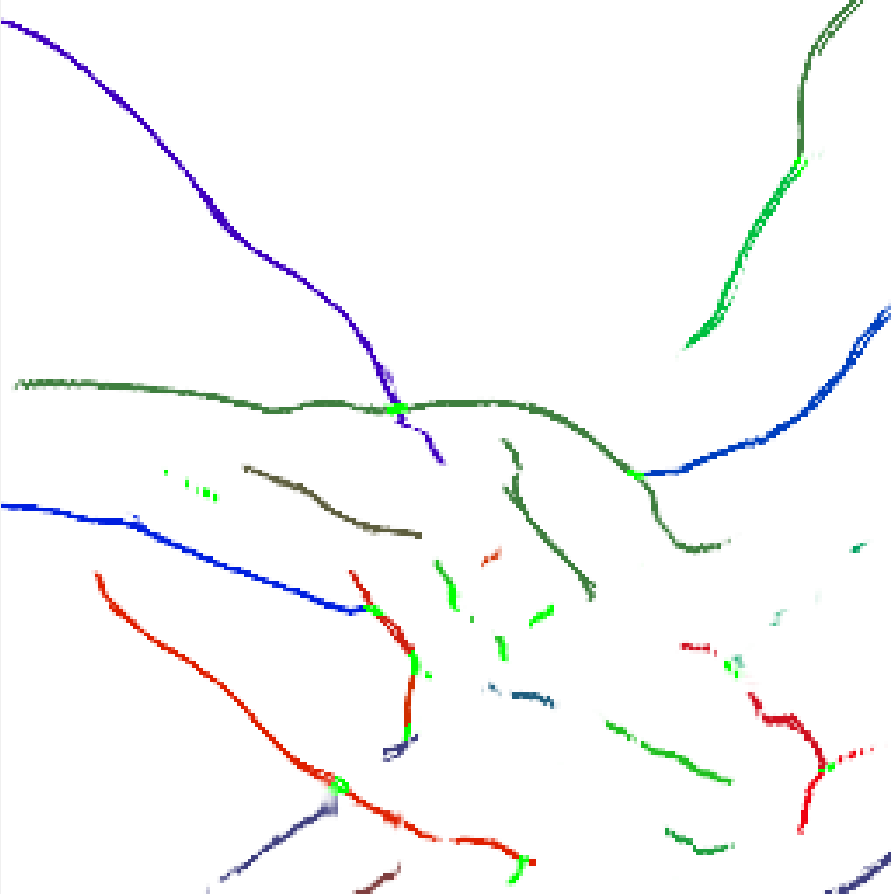

Output File

The final output should be in the form of a run length encoded csv file containing the assigned labels for the entire 3D volume. The file should be in the same format as the input run length encoded files described in the "Input Data Files" section, with the values being the assigned voxel labels.

In your labelling, all voxels which have zero probability of containing a crack should be labeled as 0. For other voxels, the label should correspond to a label number unique to the crack which this voxel is a part of. You are free to choose any positive integer between 1 and 1000 for the label of a specific crack. For example, if you choose to label a certain crack as 31, then you should label all voxels contained within this crack as 31.

Your output file must contain labels for all 102,297,600 voxels in the 3D volume, regardless of test type. Therefore, the sum over all rows of "count" values in your output file must equal 102,297,600 in order to receive a non-zero score.

Functions

During the contest, only your output file, containing the provisional and system results, will be submitted. In order for your solution to be evaluated by Topcoder's marathon match system, you must implement a class named AutoCracks, which implements a single function: getAnswerURL(). Your function will return a String corresponding to the URL of your submission file. You may upload your output file to a cloud hosting service such as Dropbox or Google Drive, which can provide a direct link to the file.

To create a direct sharing link in Dropbox, right click on the uploaded file and select share. You should be able to copy a link to this specific file which ends with the tag "?dl=0". This URL will point directly to your file if you change this tag to "?dl=1". You can then use this link in your getAnswerURL() function.

If you use Google Drive to share the link, then please use the following format: "https://drive.google.com/uc?export=download&id=XYZ" where XYZ is your file id.

Note that Google Drive has a file size limit of 25MB and can't provide direct links to files larger than this. (For larger files the link opens a warning message saying that automatic virus checking of the file is not done.)

You can use any other way to share your result file, but make sure the link you provide opens the filestream directly, and is available for anyone with the link (not only the file owner), to allow the automated tester to download and evaluate it.

An example of the code you have to submit, using Java:

public class AutoCracks
{
   public String getAnswerURL()
   {
      // Replace the returned String with your submission file's URL
      return "https://drive.google.com/uc?export=download&id=XYZ";
   }
}

After the submission phase of the contest has been completed, your last submission will be tested against the system region. The URL in your final submission must remain active and directed to the same file until system scoring has been completed and the system rankings are announced. If your URL becomes inactive, you will receive a final score of zero as we will not be able to score your results.

Keep in mind that your complete code that generates these results will be verified at the end of the contest if you achieve a score in the top 10, as described later in the "Requirements to Win a Prize" section, i.e. participants will be required to provide fully automated executable software to allow for independent verification of the performance of your algorithm and the quality of the output data.

Scoring

For example submissions, only voxels in the training region will be scored. For provisional submissions, the union of voxels in the training and provisional regions will be scored. For final system scoring, only voxels in the system region will be scored. However, you must always label all voxels in the entire 3D volume.

Only voxels with a ground truth label greater than 2 are scorable. For the training and provisional regions, all scorable voxels are only contained within the following Z-slices: z = 0, 18, 34, 51, 68, 84, 101, 118, 134, 151, 167, 184, 201, 218, 234, 250, 268, 284, 301, 318, and 332. The location of scorable voxels in the system region will not be revealed. All voxels within the 3D volume should be labeled in your final submission.

Scoring is based on the F-score metric where the value of true positives (TP), false positives (FP), and false negatives (FN) are determined by the intersection-over-union metric. Score is calculated using the following pseudocode:

TP = 0
FP = 0

for each non-zero answer label
{
   for each ground truth label greater than 2
   {
      I = num scorable voxels with both answer and ground truth label
      U = num scorable voxels with either answer or ground truth label
      IOU = I / U

      if IOU > 0.5
      {
         TP += IOU
         set ground truth label as matched
      }
      else
      {
         FP += IOU
      }
   }
}

FN = number of unmatched ground truth labels

f-score = 2 * TP / (2 * TP + FN + FP)

score = 1,000,000 * f-score

Final Scoring

The top 5 competitors with non-zero provisional scores are asked to participate in a two phased final verification process. Participation is optional but necessary for receiving prizes.

Phase 1. Code Review

Within 2 days from the end of submission phase you must package the source codes you used to generate your latest submission and send it to jsculley@copilots.topcoder.com and tim@copilots.topcoder.com so that we can verify that your submission was generated algorithmically. We won't try to run your code at this point, so you don't have to package data files, model files or external libraries, this is just a superficial check to see whether your system looks convincingly automatized. If you pass this screening you'll be invited to Phase 2.

Phase 2. Online Testing

You will be given access to an AWS VM instance. You will need to load your code to your assigned VM, along with three scripts for running it:

• compile.sh should perform any necessary compilation of the code so that it can be run. It is possible to upload precompiled code, so running compile.sh is optional. But even if you use precompiled code your source code must be uploaded as well.
• train.sh <training_data_folder_path> <model_folder_path> should create any data files that your algorithm needs for running test.sh later. All data files created must be placed in the supplied model folder. The allowed time limit for the train.sh script is 12 hours. The training data folder contains the same data as is available to you during the contest. It should be possible to skip the training step on the server and upload a model file that you created previously.
• test.sh <testing_data_folder_path> <model_folder_path> <output_file> should run the code using new, unlabeled data and should generate the output CSV file. The allowed time limit for the test.sh script is 6 hours. The testing data folder contains similar data in the same structure as in the downloaded provisional testing data. The model folder is the same as was used in the call of train.sh, so you can use any data files that were created during training.

Your solution will be validated. We will check if it produces the same output file as your last provisional submission, using the same testing input files used in this contest. We are aware that it is not always possible to reproduce the exact same results. For example, if you do online training then the difference in the training environments may result in a different number of iterations, meaning different models. Also, you may have no control over random number generation in certain 3rd party libraries. In any case, the results must be statistically similar, and in case of differences you must have a convincing explanation why the same result can not be reproduced.

Competitors who fail to provide their solution as expected will receive a zero score in this final scoring phase, and will not be eligible to win prizes.

General Notes

• This match is not rated.
• Provisional submissions are allowed once every 4 hours, while example submissions are allowed once every 15 minutes. You may use example submissions to test the format of your submission. Your last submission will be used for final scoring, so please ensure that it is properly formatted. You will not be allowed to submit after the contest submission deadline, so plan your provisional submissions accordingly.
• In this match you may use any programming language and libraries, including commercial solutions, provided Topcoder is able to run it free of any charge. You may also use open source languages and libraries, with the restrictions listed in the next section below. If your solution requires licenses, you must have these licenses and be able to legally install them in a testing VM (see "Requirements to Win a Prize" section). Submissions will be deleted/destroyed after they are confirmed. Topcoder will not purchase licenses to run your code. Prior to submission, please make absolutely sure your submission can be run by Topcoder free of cost, and with all necessary licenses pre-installed in your solution. Topcoder is not required to contact submitters for additional instructions if the code does not run. If we are unable to run your solution due to license problems, including any requirement to download a license, your submission might be rejected. Be sure to contact us right away if you have concerns about this requirement.
• You may use open source languages and libraries provided they are equally free for your use, use by another competitor, or use by the client.
• If your solution includes licensed software (e.g. commercial software, open source software, etc), you must include the full license agreements with your submission. Include your licenses in a folder labeled "Licenses". Within the same folder, include a text file labeled "README" that explains the purpose of each licensed software package as it is used in your solution.
• The usage of external resources is allowed as long as they are freely available.
• Use the match forum to ask general questions or report problems, but please do not post comments and questions that reveal information about the problem itself or possible solution techniques.

Requirements to Win a Prize

In order to receive a prize, you must do all the following:

1. Achieve a non-zero score in the top 5, according to system test results. Send your source codes for code review. See the "Final scoring" section above for details on these steps.
2. Within three (3) days of the end of the code review phase, you need to provide the copilot and administrator with VM requirements for your solution. Five (5) days from the date you receive the VM, the VM must be set up with your solution so Topcoder can easily validate and run it. Once the final scores are posted and winners are announced, the top five (5) winners have seven (7) days to submit a report outlining your final algorithm explaining the logic behind and steps to its approach. You will receive a template that helps creating your final report.

Definition

Examples