March 3, 2012
SRM 535

DURATION
25 mincategories
Tags
share
Match Summary
Round Overview
Discuss this match
March 2012, a month that has a unusually strong amount of contests, began with SRM 535. A record-breaking match with 2500 registrants! So many great coders from all over the world competing over the same goal. The division 1 problem set was not short on interesting challenges: Of almost 1000 coders, only 621 were able to get a positive score. The top 3 was this time destined to the three coders who could solve the 1000 points problem correctly: wata, tourist and ACRush. ACRush’s advantage of over 300 points over the second place was completely justified: The best score in the easy and hard problem, a very good score for the medium and seven successful challenges.
Division 2 was not without a challenging problem set either. Unfortunately, of the 1500 participants nobody could solve the hard problem correctly during the match. As a result, the top places are virtually tied, with less than 80 points of difference between 1-st and 8-th place. logic_max stood out thanks to challenge success and decent scores for the two first problems.
Used as: Division Two - Level One:
| Value | 250 |
| Submission Rate | 1310 / 1412 (92.78%) |
| Success Rate | 1073 / 1310 (81.91%) |
| High Score | OksanaZ for 249.51 points (1 mins 15 secs) |
| Average Score | 202.48 (for 1073 correct submissions) |
There are two common approaches for this problem. You could solve the equations. Note that a+b = APlusB and a-b = AMinusB make two pairs of equation that are enough to find a and b. Similarly, b+c = BPlusC and b-c = BMinusC make another pair of equations. After solving the equations (and making sure that each has a integer result, because that is one of the conditions of the problem), verify that the values of b are equal for both pairs of equations.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
vector < int > get(int AminusB, int BminusC, int AplusB, int BplusC) {
// Solve the equations
// B - A = - AminusB
// B + A = AplusB
// 2B = AplusB - AminusB
// B - C = BminusC
// B + C = BplusC
// 2B = BminusC + BplusC
if (abs(AplusB - AminusB) % 2 != 0) {
//No integer solution
return vector < int > (0);
}
if (abs(BplusC + BminusC) % 2 != 0) {
//No integer solution
return vector < int > (0);
}
int b1 = (AplusB - AminusB) / 2;
int b2 = (BplusC + BminusC) / 2;
if (b1 != b2) {
// the two values of b must match.
return vector < int > (0);
}
int a = AplusB - b1;
int c = BplusC - b2;
// Return the found result.
vector < int > v(3);
v[0] = a;
v[1] = b1;
v[2] = c;
return v;
}
This time, however, an approach like that might take quite some time to implement and debug. On the other hand, the condition that requires the solution to be integers and the small constraints for the variables make it very easy to just iterate through all possible triples (a,b,c). You can confirm through the constraints that no number in the solution can be smaller than -60 or greater than 60 (The actual bounds are smaller, even). It is also possible to simply use as large as possible values that would run in time. For each picked triple, verify if it matches the given conditions, if that is the case you have found the solution.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
vector < int > get(int AminusB, int BminusC, int AplusB, int BplusC) {
for (int a = -60; a <= 60; a++) {
for (int b = -60; b <= 60; b++) {
for (int c = -60; c <= 60; c++) {
// Verify that {a,b,c} is a solution:
if (a + b == AplusB && a - b == AminusB &&
b + c == BplusC && b - c == BminusC) {
// Return {a,b,c}
vector < int > v(3);
v[0] = a;
v[1] = b;
v[2] = c;
return v;
}
}
}
}
// No solution found. Return an empty vector
return vector < int > (0);
}
Used as: Division Two - Level Two:
| Value | 500 |
| Submission Rate | 554 / 1412 (39.24%) |
| Success Rate | 154 / 554 (27.80%) |
| High Score | ajay.verma for 465.56 points (7 mins 50 secs) |
| Average Score | 278.74 (for 154 correct submissions) |
Used as: Division One - Level One:
| Value | 250 |
| Submission Rate | 839 / 900 (93.22%) |
| Success Rate | 593 / 839 (70.68%) |
| High Score | ACRush for 247.22 points (3 mins 1 secs) |
| Average Score | 180.57 (for 593 correct submissions) |
When thinking about A and B, consider what they have in common. They are both divisors of L and they are both multiples of G. When we say that A is a multiple of G, we mean that there exists a number a such that: (a*G = A). Similarly, there exists a number b such that: (b*G = B). The value we want to minimize, A+B is then equal to (a*G + b*G) = G * (a + b). Since G is constant, we are interested in minimizing (a + b) - Note that these two numbers must not have a divisor in common, because if they did, then G would not have been the GCD of A and B.
a and b will still be divisors of L. In fact, consider the known relation: lcm(A,B) = A*B / GCD(A,B). It translates to L = A*B/G, which can translate to: L/G = A/G * B/G or: ( L/G = a * b ). This means for a given value of b, a = (L/G)/b. More than that, a and b are both divisors of (L/G). At this point, it is useful to know that it is possible to get all divisors of a number L/G in O(sqrt(L/G)) time. You can thus iterate through all divisors a of L/G, and let b = L/G/a, this is enough to find all possible pairs (a,b) (Remember though that by the first paragraph, these must be pair-wise coprime (no divisor in common)). We can then, for each of those pairs calculate a+b and then take the minimum of the values we found.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public class FoxAndGCDLCM {
//Euclid's method to get the gcd of two numbers
long gcd(long a, long b) {
while (b != 0) {
long c = b;
b = a % b;
a = c;
}
return a;
}
public long get(long G, long L) {
// Before dividing L/G, make sure L is a multiple of G.
if (L % G != 0) {
return -1;
}
long res = -1;
long ab = L / G;
// divisors of ab
// For each pair (a,b) such that a*b == ab,
// at least one of the (a,b) will be <= sqrt(ab)
for (long a = 1; a <= ab / a; a++) {
if (ab % a == 0) {
//try all pairs (a,b)
long b = ab / a;
if (gcd(a, b) == 1) { //pair-wise coprime?
long apb = (a + b) * G;
if (res == -1) {
res = apb;
} else {
res = Math.min(res, apb);
}
}
}
}
return res;
}
}
Used as: Division Two - Level Three:
| Value | 1000 |
| Submission Rate | 8 / 1412 (0.57%) |
| Success Rate | 0 / 8 (0.00%) |
| High Score | null for null points (NONE) |
| Average Score | No correct submissions |
In problems that ask you for the idx-th element of a sorted sequence (where just simulating creating a sorting the sequence would time out), it tends to be productive to turn the problem into a counting problem. Let us say we wish to build the number given by the idx index. Since the sequence is sorted, there are different kinds of elements, and some come before others. In this case, the main attribute to sort is the sum of the digits. Let us estimate the sum of digits of element #idx:
The first sum of digits possible is 0, the single element with 0 as sum of digits will be the first of the sequence. This means that if idx is 1, then the sum of digits will be 0. What if idx is greater than 1? Then we can say that the element we are looking for is the (idx - 1)-th among the remaining elements in the sequence (those without 0 as sum of digits). We can just set (idx = idx - 1).
We can go on, there are 18 elements with a sum of digits equal to 1. If the new idx is less than or equal to 18, then we can assume it is one of the 18 elements with sum = 1. Else it will be the (idx - 18)-th number with a sum of digits greater than 1. We can continue this logic until we find two things a) The sum of the digits of the wanted number. And b) The index of the wanted number with respect to the numbers with that sum of digits (ignoring all numbers with fewer sums).
After the sum of the digits is found, we can continue using the logic to get the actual digits as well. This time, it depends on the lexicographically ordering of the numbers. This means that numbers that begin with 0 come before those that begin with 1, which come before those that begin with digit 2, and so and so. Once again, count the number of elements of the required sum that begin with 1 (In the case of the first digit, it cannot be 0). If this number is greater than or equal to idx, then you can tell that this is the number the wanted element will begin with, else subtract the amount from idx to find the index of the number among the numbers that begin with a digit greater than 1. You can continue trying digits until you find a) The starting digit of your number and b) The index of the number in respect to the elements that begin with that digit. However, you should note that once a digit is picked, the wanted sum of digits will be reduced by the value of the digit.
For the second digit, the logic works almost the same way, there is a small difference and it is that it is possible to terminate the number and also to place 0 as a digit. The lexicographical order rules in the statement assert that “1” comes before “10”, or that “” comes before “0”. In other words, you have to first count the number of elements with the wanted sum that do not contain any digits. (There is at most one of them, when the sum is 0). Then count the number of elements that start with 0, then those that start with 1, and so and so until you find whether the number finishes (empty), or has a digit in the second position (and in that case, you would also like the relative index in regards to the numbers that have that digit in the second position.
This process can be repeated for all the remaining digit positions until we find a case that picks empty digits for the remaining positions. Due to the problem statement, there are at most 18 digit positions (the largest number in the array has 18 ‘9’ digits.).
What we do need now is a way to count the number of elements that follow each of the required conditions. We need a function that is able to count the total number of elements of up to 18 digits that have a certain sum of digits. We also need to know how to count the specific values for elements that begin with a given digit. We will adapt the same function to do both things.
Let us think of a function f(S, 18) that gives the total number of elements that have a digit sum equal to S and at most 18 digits. The latter condition is needed to allow us to count numbers that actually have less than 18 digits. We would like to solve f(S, x) for any pair of valid values of s and x. It can work as a recurrence:
If x = 0, then we can use at most 0 digits. Which is the same as using no digits at all. In other words the sum must be 0. If the sum is 0, then there is 1 (empty) sequence that solves the problem, else there is none. This will be our base case.
When x is not 0, we must first verify if there is an empty sequence that solves the condition. This happens when S=0 (The sum of digits of an empty sequence is 0).
Else we would like to use one of the 10 available digits. Note that we cannot use 0 for the first digit (to avoid leading zeros), so we can only use 0 when x is less than or equal to 18. Let us say we picked digit d: Then the sum of the remaining digits must be (S-d), and there are (x-1) digits left. This yields f( S - d, x-1), The sum of this recursive instance for each valid digit d, is the result of the recurrence relation.
In order to calculate this function quickly, we can use Memoization. After calculating the result for each (s,x), save the value of the result so that you no longer have to need to calculate the number again. This will ensure a O( max_sum, max_digits ) complexity (The 10 factor caused by the 10 digits is constant).
In order to calculate the number of ways to start with a digit d, simply remember that after using the digit, both the required sum and the digit number would change. The sum changes to (sum - d), whilst the digit number to (x - 1), so we can just call f(S - d, x - 1) to find this required number.
By combining the counting algorithm and the construction algorithm, and tweaking some final details we can solve the problem:
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
public class FoxAndSorting {
final int MAX_DIGITS = 18;
// dp[s][x] : The total count of numbers with at most x digits
// with a digit sum equal to s
long[][] dp;
long rec(int s, int x) {
if (dp[s][x] == -1) {
long res = 0;
if (s == 0) {
// The empty number is a valid result
// as its sum of digits is 0.
res++;
}
// Pick a digit from 0 (if possible) to 9
for (int d = 0;
(d <= 9) && (s - d >= 0); d++) {
if ((x != 0) && ((d != 0) || (x != MAX_DIGITS))) {
res += rec(s - d, x - 1);
}
}
dp[s][x] = res;
}
return dp[s][x];
}
public long get(long idx) {
// initially the dp array to -1 for the recursion to work.
dp = new long[163][MAX_DIGITS + 1];
for (int i = 0; i < 163; i++) {
for (int j = 0; j <= MAX_DIGITS; j++) {
dp[i][j] = -1;
}
}
int s = 0;
while (idx > rec(s, MAX_DIGITS)) {
idx -= rec(s, MAX_DIGITS);
s++;
}
long num = 0;
for (int x = 18; x >= 1; x--) {
if (s == 0) {
// If the required sum for the remaining digits is 0,
// then there exists a result that has no more digits
// left. This result has lexicographical priority over
// the rest (its index is 0).
if (idx == 1) {
break;
} else {
//it is not the empty number, forget it.
idx--;
}
}
// Try each digit from 0 (if possible) to 9.
for (int d = 0;
(d <= 9) && (s - d >= 0); d++) {
if ((d != 0) || (x != MAX_DIGITS)) {
if (idx <= rec(s - d, x - 1)) {
// The current index is such that it should belong
// to the numbers that begin with x.
num = num * 10 + d;
s -= d;
break;
} else {
// update the index to forget about the numbers with
// the previous digits.
idx -= rec(s - d, x - 1);
}
}
}
}
return num;
}
}
Used as: Division One - Level Two:
| Value | 500 |
| Submission Rate | 316 / 900 (35.11%) |
| Success Rate | 73 / 316 (23.10%) |
| High Score | wcao for 442.13 points (10 mins 33 secs) |
| Average Score | 260.44 (for 73 correct submissions) |
We often believe time is an important thing. But maybe such thing is not so true in some cases. Let us first state that for any set of K employees you pick, there will always be a time t that each employee can work so that the final result is exactly totalWork. Let a[x], a[y], a[z], … be the abilities of the K employees. The time each employee works is t. Then we have that the total amount of work is totalWork = t*(a[x] + a[y] + …). As a[] contains only positive numbers, there is always a solution for t.
Why is that important? Mostly because we are not interested in minimizing or maximizing time spent. We are minimizing cost. It is true that the time will have an effect in the machine renting cost, but we can handle it without calculating the time. Let us measure time in hours, for every hour assigned to a single employee, the rent costs 3600 yen.
Another important thing of note, it does not matter how much time you assign to each employee. As the times are all equal, the proportions between the amounts of products created by each employee will remain the same. For example, if we pick employees x and y. Then for every unit produced by x, y will always produce a[y]/a[x] units. Let us now calculate how much we spend on a single employee per hour: For employee x, the result is a[x]*p[x].
What does matter is the total cost. Note that given a total cost, it will involve some cost per unit of work done. Since totalWork is constant, we in fact can change the problem to minimizing the average amount of cost per unit. As this cost per unit will not necessarily be integer, it is probably best to try to use a binary search algorithm. In order to do that, let us analyze how to answer the question : Can I pay M yen in average for each unit of work?: If you cannot pay M yen in average, you cannot pay a smaller value than M. If you can pay M in average then you can pay also a larger value than M. This means that the question can be answered with a binary search.
In order to answer the question, remember that we calculated the amount of yen you need to make a single employee work for an hour and also the amount of yen required for the machine for a single of the K employees during an hour. If we are paying M yen per unit of work then we will be paying (a[x] + a[y] + …) * M yen in total during an hour. A cost rate M is valid if (a[x] + a[y] + …) * M is enough to cover both expenses (a[x]*p[x] + a[y]*p[y] + … + K * 3600).
1
M * (a[x] + a[y] + ...) >= (a[x] * p[x] + a[y] * p[y] + ...) + K * 3600.
Note that we must pick the employees x,y, … in a way such that the inequality has a better chance to be true. Since K * 3600 is constant, this means that we would like M*(a[x] + a[y] + … ) - (a[x]*p[x] + a[y]*p[y] + …) to be as large as possible.
1max(M * (a[x] + a[y] + ...) - (a[x] * p[x] + a[y] * p[y] + ...)) = max(M * a[x] - a[x] * p[x]) + max(M * a[y] - a[y] * p[y]) + ...
Since we would like to pick K employees such that the objective is as large as possible, we should pick the K employees with the largest ( M*a[i] - a[i]*p[i] ). This can be done easily by sorting.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
double minimumCost(int K, int totalWork, vector < int > a, vector < int > p) {
int n = a.size();
double lo = 0, hi = 1e20;
// When binary search is done in a floating point space, it
// is better to do a fixed number of iterations
for (int iter = 0; iter < 1000; iter++) {
double M = (lo + hi) / 2;
vector < double > v(n);
for (int i = 0; i < n; i++) {
v[i] = a[i] * M - a[i] * (double) p[i];
}
// sort the array of values in non-descending order
sort(v.rbegin(), v.rend());
double sum = 0;
// pick the k best ones
for (int i = 0; i < K; i++) {
sum += v[i];
}
// Check sum >= K*3600 (equivalent to M*sum(a[i]) >= sum(a[i]*p[i]) + K*3600
if (sum >= K * 3600) {
// valid, thus we know that the upper bound is at most M
hi = M;
} else {
// invalid, the lower bound is at least M
lo = M;
}
}
// The result is the minimum (cost / work) rate multiplied by totalWork
return hi * totalWork;
}
Used as: Division One - Level Three:
| Value | 1000 |
| Submission Rate | 8 / 900 (0.89%) |
| Success Rate | 3 / 8 (37.50%) |
| High Score | ACRush for 711.63 points (19 mins 51 secs) |
| Average Score | 550.57 (for 3 correct submissions) |
At times, the difference between solving a problem and not solving it lies between how you analyze it. In this case, it is very helpful to see that the movement caused by the greedy algorithm is split in two phases. In the first phase, you must always decide between two cells. Eventually, you will reach the right-most column or the bottom-most row and no longer have any decision to make - instead you will just move directly to the bottom-right corner. Note that you will almost always reach a cell in the bottom-most row or right-most column that is not the final cell.
There are some corner cases in which this analysis is not so true. They are those case in which there is only one column or one row, this time the first phase is not present and you start in cell (0,0) instantly. These cases are easier to deal with separately though, and from now we will focus only in the case where both dimensions are at least 2.
We are counting grids, but now that we have made the analysis, we can say that the grids in which the greedy path goes to the bottom-most row before reaching (H-1, W-1) are all different to the grids with a greedy path that reaches the right-most column first. We can then break the problem into a) Counting the grids that go through the bottom-most row. and b) Counting the grids that go through the right-most column. You can suspect these problems are very similar, and they are. So we will now focus on a).
When solving a), there are W-1 possible cells in the bottom-most row that the second phase can start in. Once again, a grid such that the second phase begins at cell (H-1, i) is different than another grid in which the second phase begins at cell (H-1, j) (For i!=j). (Once again, the second phase cannot start at cell (H-1,W-1).) There are at most 2499 of these cells. So, for now let us assume we will solve for each value of i and then add all the results together to find the final result for a).
We now want to count all the grids such that the second phase begins at cell (H-1, i). We cannot do this in a lot of time because this process will be repeated for up to 2499 values of i. Note that a grid’s greedy path is only determined by few cells in the grid. The remaining cells in the grid will be able to have any value. Let us try to find, for the given i how many cells are relevant to the path. Second phase is easy: There are (W - i - 1) cells that you must visit after reaching cell (H-1, i) (All in the bottom-most row) let us call this value forced. There are more cells related to phase 1. Note that it does not matter what happens to the greedy algorithm, in order to reach cell (H-1, i), it will always perform the same number of horizontal and vertical moves. Let us count the number of horizontal moves and vertical moves we will have to do in phase 1: The number of horizontal moves, horz is equal to i. The number of vertical moves, vert is equal to (H-1). Another important cell is (0,0) which will always have 0 as value.
Now note that each move in phase 1 involves deciding between 2 cells. One of the cells will be used, while the other discarded. Once a cell is discarded, we will never have the chance to visit it again nor have to use it in a decision. For each of the horz horizontal moves, there are 2 important cells. The cell you decide to visit and the cell you decide not to visit. The same happens for the vertical moves. Each vertical move has two cells as well. Note that cell (H-1, i*) is used by the last vertical move.*
Let us name the number of cells that can have any value. It will be (free = WH - 1 - 2horz - 2*vert - forced). For every kind of greedy path we find that goes through cell (H-1, i), there will be (S+1)freeways to set the numbers for the free cells.
Let us now count the number of different greedy paths. Let us first focus on the number of ways to pick the cells related to horizontal moves and those for vertical moves:
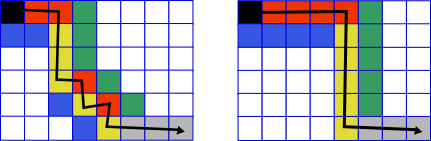
In the graphics, there are two greedy paths that end in a cell (H-1, i) (This time i is 4, H is 6 and W is 8). The red cells are cells visited in horizontal moves, blue cells are discarded by horizontal moves, yellow cells visited by vertical moves, green cells are discarded by vertical moves. The gray cells are visited in the second phase. Besides of explaining the previous few paragraphs, the intent of the image is to show that the total number of ways to distribute the important cells is equivalent to the total number of grid paths between (0,0) and (H-2, i). Counting these paths is a known problem and is the same as counting the number of ways to pick (horizontal moves) elements out of (vertical moves + horizontal moves) total elements (The vertical moves not counting the last one between (H-2, i) and (H-1, i). In other words, Binomial(horz + vert - 1, horz ).
We know the number of ways to decide the positions of the important cells and the number of ways to fill the non-important cells. We still need to know the number of ways to put values in the cells themselves such that the total sum of the visited cells is S. There are two phases and each will yield a different part of the sum of visited cells. Let us say that the sum of the cells visited in phase two is c. Then there will be free cells on which we can put any value from 0 to S such that the total sum is c. This is a typical dynamic programming problem, let us say that a function called f3( free, c) will return the number of ways to put values in these cells. There are still a sum of (S - c) to be accomplished by the first phase. Say a is the amount summed by cells reached by horizontal moves and b the amount summed by cells reached by vertical moves (a + b + c = S). Each horizontal and vertical move is related to two cells. For each pair of these cells, you have to decide two values (x,y) x is the value in the cell visited by the move and y the one discarded by it. In the case of horizontal moves (x >= y), in the case of vertical moves (x > y) (This is due to the conditions used by the greedy algorithm, it visits the greatest of two cells, or the right one if the two are equal). The number of ways to value the cells related to horizontal moves is equal to the number of sequences of pairs (x,y) such that the total sum of x is a and (x >= y), we will call this function f1( horz, a). Similarly, there is a function f2( vert, b) for the vertical moves. These two functions are also easily solvable by dynamic programming, using a variation of the algorithm for f3 that multiplies for each picked x the corresponding amount of possible options of y.
Note that f3 can also solve the special case in which one of the dimensions of the grid is 1. As it counts the number of sequences that give a sum equal to S.
The sum of all the products of the functions for each triplet (a,b,c) (a + b + c = S), multiplied by the remaining factors (the binomial, the power of the free cells), will yield the number of grids with a path that visits cell (H-1, i). The sum of all these values will yield the number of grids such that their paths visit the bottom-most row. You will see that the right-most column can be solved in the same manner for each j < H-1, and in fact will use the same functions f1, f2, f3 (The only difference is when counting the number of horizontal and vertical moves, and the number of paths, this time a horizontal move is forced to be the last one). Since we can assume the dynamic programming functions were precalculated, this gives us a O( W* S*S + H*S*S) algorithm. S is at most 100, so this is viable. The run time will be very tight though. There are some low level optimizations we can do. For example, there are many operations that do not need to be done for each triplet (a,b,c) and can be done for each i (or j). It is also a good idea to avoid performing the mod operation too frequently. The following Java code takes around 1 second in the worst case:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
public class FoxAndGreed {
final int MOD = 10007;
int modpow(int x, int y) {
int r = 1, a = x;
while (y > 0) {
if ((y & 1) == 1) {
r = (r * a) % MOD;
}
a = (a * a) % MOD;
y /= 2;
}
return r;
}
int[] fact;
int[] invfact;
int binomial(int n, int k) {
// n! / (k! * (n-k)!)
int p = fact[n];
p = (p * invfact[k]) % MOD;
p = (p * invfact[n - k]) % MOD;
return p;
}
int[][] f1, f2, f3;
//(sum of: f1[horz][a]*f2[vert][b]*f3[forced][c]) for all (a,b,c): a+b+c = S
public int subProblemSum(int horz, int vert, int forced, int S) {
int r = 0;
for (int a = 0; a <= S; a++) {
for (int b = 0; a + b <= S; b++) {
int c = S - b - a;
// this code is called plenty of times.The if (p>=MOD) checks
// help reduce the number of divisions performed.
int p = f1[horz][a];
p *= f2[vert][b];
if (p >= MOD) p %= MOD;
p *= f3[forced][c];
if (p >= MOD) p %= MOD;
r += p;
if (r >= MOD) r %= MOD;
}
}
return r;
}
public int count(int H, int W, int S) {
f1 = new int[H + W + 2][S + 1];
f2 = new int[H + W + 2][S + 1];
f3 = new int[H + W + 2][S + 1];
//f1[t][s] : Counts sequences of t pairs (x,y) such that:
// sum(x) = s
// (x >= y) for all elements.
//...
//f2[t][s] : Counts sequences of t pairs (x,t) such that:
// sum(x) = s
// (x > y) for all elements.
//...
//f3[t][s] : Counts sequences of t elements x such that:
// sum(x) = s
//...
f1[0][0] = f2[0][0] = f3[0][0] = 1;
for (int t = 1; t <= H + W + 1; t++) {
for (int s = 0; s <= S; s++) {
f1[t][s] = 0;
f2[t][s] = 0;
f3[t][s] = 0;
for (int x = 0; x <= s; x++) {
f1[t][s] += f1[t - 1][s - x] * (x + 1);
f2[t][s] += f2[t - 1][s - x] * x;
f3[t][s] += f3[t - 1][s - x];
}
f1[t][s] %= MOD;
f2[t][s] %= MOD;
f3[t][s] %= MOD;
}
}
if (Math.min(W, H) == 1) {
return f3[W * H - 1][S];
}
// { W>=2 && H>=2 }
// Precalculate factorial and its inverse
fact = new int[H + W + 2];
invfact = new int[H + W + 2];
fact[0] = 1;
invfact[0] = 1;
for (int i = 1; i <= H + W + 1; i++) {
fact[i] = (fact[i - 1] * i) % MOD;
invfact[i] = modpow(fact[i], MOD - 2); //Fermat's little theorem
}
int res = 0;
// a) Count grids with the move (H-2, i) -> (H-1, i)
for (int i = 0; i <= W - 2; i++) {
int horz = i;
int vert = H - 1;
int forced = W - i - 1;
int free = W * H - 1 - forced - 2 * horz - 2 * vert;
int q = (binomial(horz + vert - 1, horz) * modpow(S + 1, free)) % MOD;
// q * (sum of: f1[horz][a]*f2[vert][b]*f3[forced][c]) for all (a,b,c): a+b+c = S
q = (q * subProblemSum(horz, vert, forced, S) % MOD);
res = (res + q) % MOD;
}
// b) Count grids with the move (j, W-2) -> (j, W-1)
for (int j = 0; j <= H - 2; j++) {
int horz = W - 1;
int vert = j;
int forced = H - j - 1;
int free = W * H - 1 - forced - 2 * horz - 2 * vert;
int q = (binomial(horz + vert - 1, vert) * modpow(S + 1, free)) % MOD;
// q * (sum of: f1[horz][a]*f2[vert][b]*f3[forced][c]) for all (a,b,c): a+b+c = S
q = (q * subProblemSum(horz, vert, forced, S) % MOD);
res = (res + q) % MOD;
}
return res % MOD;
}
}