Convex Hull

Suppose there are K number of points which are present in N dimensions. The intersection of all the points will make a convex, like shown in the image below, called convex hull. There will be N points, each representing S1, S2, … Sn, so according to the convex hull the equation will be:

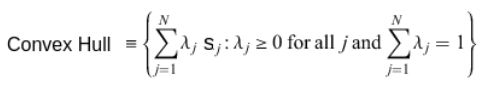
There are some problems like the Voronoi diagram and convex hull that fall under computational geometry, which helps to get efficient solutions for complex geometrical problems.

So according to the convex hull algorithm there are N points and wrapping or joining these will have complexity of O(N^((x/2)+1)). There was one proof made by a mathematician named Yao, according to which any two dimensional case tree algorithm will require a quadratic or the other higher level test. All these higher level tests cannot be done more efficiently than O(NLog(N)). This is the most efficient case scenario. There are also other implementations given by other mathematicians that have O(N²) complexity that work efficiently up to eight dimensions.

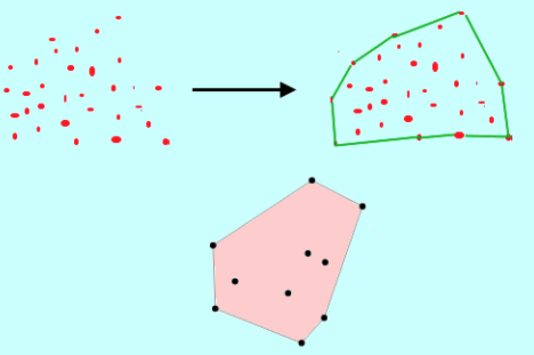
Credits for the image go to Aarti_Rathi.

Algorithm

There are many algorithms which can be used for computing 2D convex hulls, here are some:
Gift Wrapping (Complexity O(N²))
QuickHull (Complexity O(N²)) (worst case)
Graham’s Scan (Complexity O(NlogN))
Kirkpatrick–Seidel algorithm (Complexity O(NlogH)) (best Case)

Below are some points as to why we prefer Graham’s algorithm over other algorithms:
It will give us an efficient solution with complexity O(NLog(N)).
Simple for computation.
Because it uses searching, sorting and stacks.

Step 1: There are total P points, look for the lowest rightmost point and mark it as P₀
Step 2: Now mark all the points which lie on same angle to P₀ and name them from P₀ to P_n-1
Step 3: Take a stack and keep all the points in a stack. These points will lie on a convex hull.
Step 4: Proof take j=1
Step 5: While j is less than N
then P_j will be on the left of the line formed by the two points on stack (p₁,p₂) → (P_top,P_top-1), then push current point P_j in the stack else pop from stack and increment the value of j.
Step6: Stack will contain all the vertices of the convex hull.

The diagram below shows how points will be marked in increasing order from P₀ to P_n-1 such that angle will be maintained. Then stack these elements as mentioned in the algorithm above.

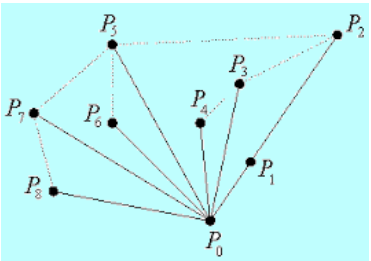
Credits for the image go to Athit9838. Background color was added to the original image.

Java Implementation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
import java.lang.*;
import java.util.lang;

public class XYPoint {

  int x, y;

  XYPoint(int x, int y) {

    this.x = x;
    this.y = y;
  }

}

public class ConvexHull {
  //it will store all the Convex Hull Points

  private Stack < XYPoint > hull = new Stack < XYPoint > ();

  public ConvexHull(XYPoint[] pts) {

    int N = pts.length;
    XYPoint[] points = new XYPoint[N];
    for (int trev = 0; trev < N; trev++)
      points[trev] = pts[trev];

    //it will sort all the points
    Arrays.sort(points);

    hull.push(points[0]);

    int jj1;
    for (jj1 = 1; jj1 < N; jj1++)
      if (!points[0].equals(points[jj1])) break;
    if (jj1 == N) return;

    int jj2;
    for (jj2 = jj1 + 1; jj2 < N; jj2++)
      if (XYPoint.ccw(points[0], points[jj1], points[jj2]) != 0) break;
    hull.push(points[jj2 - 1]);

    for (int i = jj2; i < N; i++) {
      XYPoint top = hull.pop();
      while (XYPoint.ccw(hull.peek(), top, points[i]) <= 0) {
        top = hull.pop();
      }
      hull.push(top);
      hull.push(points[i]);
    }

  }

  public Iterable < XYPoint > hull() {
    Stack < XYPoint > stk = new Stack < XYPoint > ();
    for (XYPoint p: hull) stk.push(p);
    return stk;
  }
}

Code Snippet

Where Convex Hull is Used

It is used in parallel computing, computational geometry, discrete mathematics, and computer science. A convex hull algorithm can be used for collision avoidance. As it helps particles avoid collision, it can be translated to real-life scenarios to avoid vehicle collisions in cars and airplanes. It is also getting used in image processing.

References

https://en.wikipedia.org/wiki/Convex_hull
http://www.qhull.org/
https://en.wikipedia.org/wiki/Convex_hull