Flatten Binary Tree to Linked List

About the Problem:

In this problem, we are provided with the root of the binary tree and we should use the same BinaryTreeNode to flatten the binary tree (i.e, in-place ). Each right pointer should point to the next node, the left should be NULL, and the list should be in pre-order traversal format.

Structure of BinaryTreeNode

1
2
3
4
5
6
7
8
9
10
struct Treenode {
  int val;
  Treenode * left, * right;
};

Structure of LinkedListNode
struct ListNode {
  int val;
  ListNode * next;
};

Example 1:
Input: [2,3,4,5,6,null,9,8]

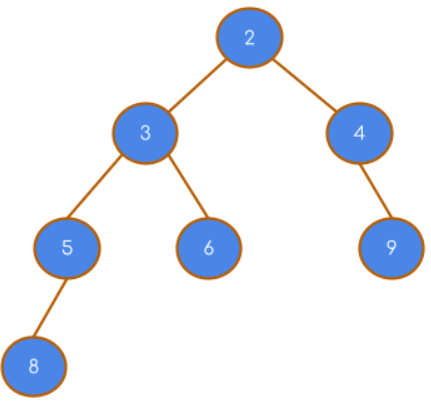
Output: [2,null,3,null,5,null,8,null,6,null,4,null,9]

Example 2:
Input: [5,7,10,null,4,null,12,11,3,4,6,7]

Approach #1: Recursion

In this approach, we are going to use post-order traversal where we visit left, right, and then the root. This is very convenient when we have to deal with links because we go from bottom to top, fixing the bottom then going up. Here we have all left nodes as NULL, therefore we change our order, i.e, we go right, left, then root.

Algorithm:

1. Declare a variable prev, to keep track of the previously visited node.

2. Pass the root node to function flatten and check where it’s NULL or not if NULL returns.

3. Make a recursion call for the right subtree and the same for the left subtree.

4. To flatten the binary tree, we first set the right pointer to the previously visited node and left to NULL.

5. Set the prev to the current node.

Code Implementation:

1
2
3
4
5
6
7
8
9
10
11
12
Treenode * prev = NULL;

void flatten(Treenode * root) {
  if (!root)
    return;
  flatten(root - > right);
  flatten(root - > left);

  root - > right = prev;
  root - > left = NULL;
  prev = root;
}

Time complexity: O(n), for visiting all the nodes in the tree once.
Space complexity: O(n), we are making a recursion call for every node in the tree.

Approach #2: Stack

In this approach to counter our call stack, we will use an explicit stack.

Algorithm:

1. Push the root node into an empty stack.

2. Run the while loop until the stack isn’t empty.

3. Pop the top node, check for its right and left child, and push them into the stack.

4. If the stack isn’t empty, set the proper child of the present popped node to the top of the stack and left to NULL.

Code Implementation:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void flatten(Treenode * root) {
  if (!root)
    return;
  stkack < Treenode * > stk;
  stk.push(root);

  while (!stk.empty()) {
    TreeNode * curr = stk.top();
    stk.pop();
    if (!curr - > right)
      stk.push(curr - > right);
    if (!curr - > left)
      stk.push(curr - > left);
    if (!stk.empty())
      curr - > right = stk.top();

    curr - > left = NULL;
  }
}

Time complexity: O(n), for visiting all the nodes in the tree once.
Space complexity: O(n), for storing all the nodes in the stack.

Approach #3: Iterative ( Space Efficient )

This approach works in O(1) space complexity. If we observe the resultant tree, every right child points to the next node of a pre-order traversal. In the case where there is no left child we only have to handle the right child. And if the left child exists, then the immediate next element in the pre-order traversal is the left child. In simpler terms, the right subtree comes right after the rightmost node in the left subtree in the pre-order traversal.
Here we find the rightmost node in the left subtree and assign the right subtree to its right child. Make the left child the right child and traverse to the next node.

Algorithm:

1. Make a curr node pointing to root and do a while loop until not equal to NULL.

2. Now check if it has a left child,
   a. If yes, traverse to the rightmost node in the left subtree
   b. Now set the rightmost node right child to curr right
   c. And curr right to curr left and left to NULL

3. Now move to the right subtree.

Code Implementation:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void flatten(Treenode * root) {
  Treenode * curr = root;
  while (curr != NULL) {
    if (curr - > left != NULL) {
      Treenode * prev = curr - > left;
      while (prev - > right)
        prev = prev - > right;
      prev - > right = curr - > right;
      curr - > right = curr - > left;
      curr - > left = NULL;
    }
    curr = curr - > right;
  }
}

Time complexity: O(n), for visiting all the nodes in the tree once.
Space complexity: O(1) only one variable is used.