Snakes and Ladders Problem

About the problem:

Like a traditional snakes and ladders game, we are provided with a 10*10 board numbered from one to one hundred and dice with faces numbered from one to six. We start from square one, and the game is considered finished when a player reaches square one hundred.

Covering two other aspects of snakes and ladders we are given two vectors of vector ladder and snake where,

• ladder[i][0] denotes the starting square of the ith ladder and ladder[i][1] denotes the end of the ith ladder.

• snake[i][0] denotes the mouth of the ith snake and snake[i][1] denotes the tail of the ith snake.

Now we are required to find the minimum number of rolls to reach the hundredth square.

Example 1:

Input: ladder = [[14,28],[42,78],[55,97],[52,92]]

snake = [[99,25],[88,54],[29,10]]

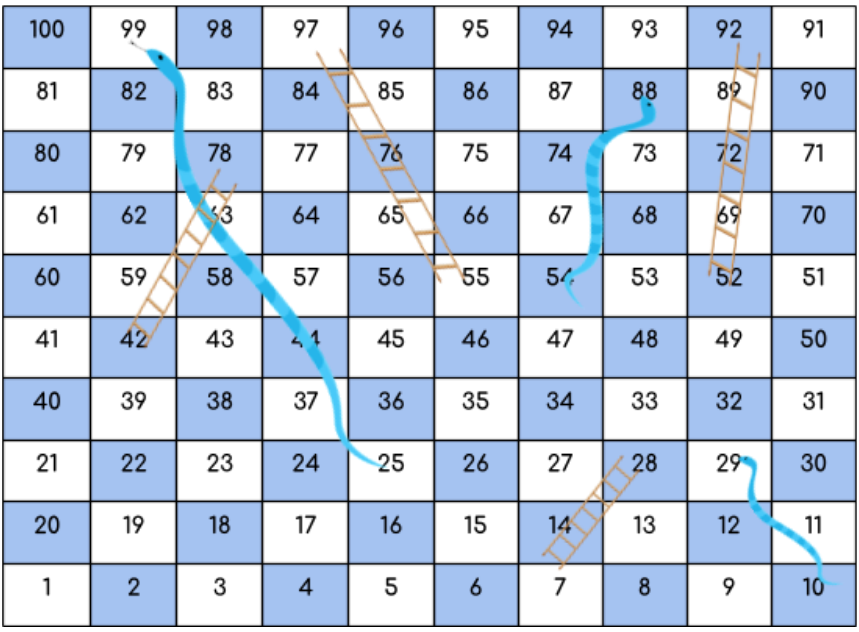
Output: 9

Example 2:

Input: ladder = [[6,46],[19,43],[52,71],[57,98]]

snake = [[47,9],[62,40],[96,75]]

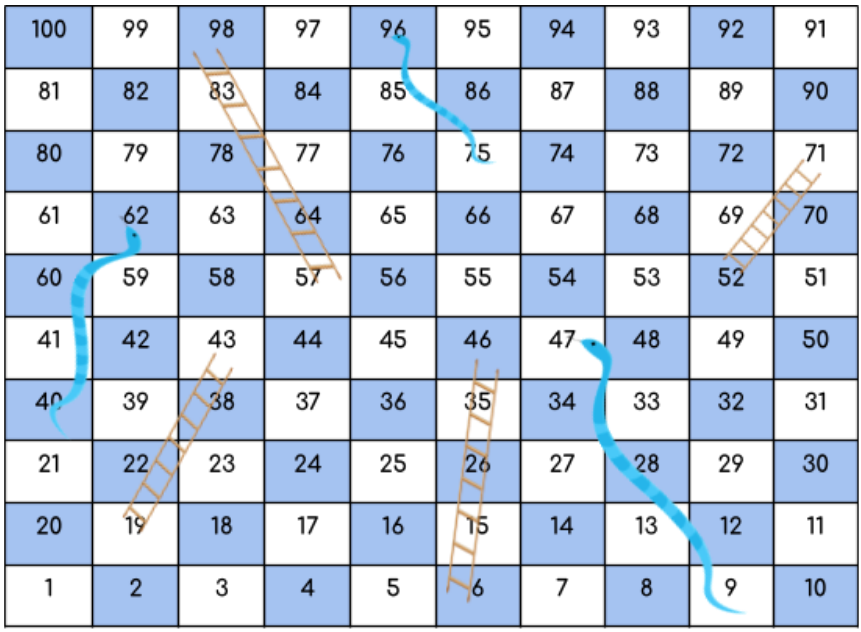
Output: 4

Approach: Breadth-First Search (BFS)

For this approach, we consider the board a graph and every square as the vertex of the graph. Here our starting vertex is one, and one hundred is the final, or destination, vertex. So, since there are six faces on a dice, we have six possible squares to move to from a particular square.

If we encounter ladder i, then it would take us from ladder[i][0] to ladder[i][1] in zero moves. Likewise, If we encounter a snake j, then it would take us from snakeji][0] to snake[j][1] in zero moves.

To note these details we are using an unordered map like below:

1
2
3
4
5
6
unordered_map < int, int > m;
for (vector < int > & i: ladder)
  m[i[0]] = i[1];

for (vector < int > & i: snake)
  m[i[0]] = i[1]

Coming to the core approach we do a level order search using BFS, where we push all possible positions in a queue, and in the next iteration loop over only the next level positions, and increment the final answer with the increasing levels in the algorithm.

Algorithm:

1. Create an explicit map and insert the ladder, snake jumping possibilities.

2. Now declare a queue and a variable level incremented with 1.

3. Now push 1 to queue and start doing a level order search.

4. Calculate the size of the queue and traverse on each possible value.

5. The new position will be x + i (1<=i<=6) if x+i is a value in map then we move to that like pos = m[x+i].

6. If the new value is 100 then we return the variable level.

7. Otherwise if the new position was not visited before then we mark it visited and push it into the queue.

8. If we are out of queue then we return -1.

Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include<bits/stdc++.h>

using namespace std;

int snakeLadder(vector < vector < int > > & ladder, vector < vector < int > > & snake) {
  unordered_map < int, int > m;
  for (vector < int > & i: ladder)
    m[i[0]] = i[1];

  for (vector < int > & i: snake)
    m[i[0]] = i[1];

  queue < int > q;
  q.push(1);
  int level = 1;
  vector < bool > vis(101, 0);
  while (!q.empty()) {
    int size = q.size();
    while (size--) {
      int x = q.front();
      q.pop();
      for (int i = 1; i < 7; i++) {
        int finalpos = x + i;
        if (m.count(x + i))
          finalpos = m[x + i];

        if (finalpos == 100)
          return level;

        if (!vis[finalpos]) {
          vis[finalpos] = 1;
          q.push(finalpos);
        }

      }
    }
    ++level;
  }
  return -1;
}

int main() {
  int s, l;
  cin >> l;
  vector < vector < int >> snake, ladder;

  int st, en;
  for (int i = 0; i < l; i++) {
    cin >> st >> en;
    ladder.push_back({
      st,
      en
    });
  }

  cin >> s;
  for (int i = 0; i < s; i++) {
    cin >> st >> en;
    snake.push_back({
      st,
      en
    });
  }

  cout << snakeLadder(snake, ladder);
}

Input:
4 6 46 19 43 52 71 57 98
3 47 9 62 40 96 75

Output:
4