Getting Started with Hash Table Data Structure - Introduction

We are going to learn all about the hash table in several articles. To begin with we will discuss what hashing is, hash tables, and other functions related to it. But our main focus in this article will be on separate chaining.

What is a Hash Table?

A hash table (HT) is a data structure that provides a mapping from keys to values using a technique called hashing.

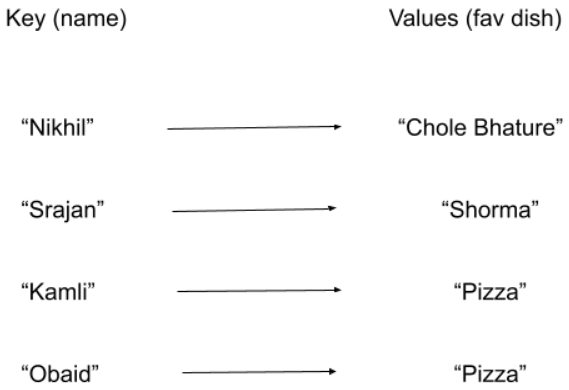
What you see above are called key-value pairs. (Don’t mind the choice of name and dishes, just some of my friends.) Keys should be unique, but values can repeat themselves.

As you can see, every key is different, but Kamli and Obaid have the same value, “Pizza”, which is valid.

HTs are often used to track item frequencies. For instance, counting the number of works in a given text. The key-value pairs don’t have to be just strings and numbers, they can also be objects. However, the keys need to be hashable, which will be discussed shortly.

Now to understand hashing better and how mapping constructs between key-value pairs we should get some idea of hash functions.

A hash function H(x) is a function that maps a key ‘ x ’number in the given fixed range.

For example, H(x) = x^2 -8x + 20 mod 8 maps all the integers keys to the range [0,7].

H(6)   =  ( 36 - 48 + 20 )  mod 8 = 0

H(0)   =      ( 0 - 0 + 20 )  mod 8 = 4

H(2)   =     ( 4 - 16 + 20 ) mod 8 = 0

H(-4)  =  ( 16 + 32 + 20 ) mod 8 = 6

We can also use arbitrary objects such as strings, lists, characters, or multiple data objects to define hash functions. There are existing examples that we can observe like the ASCII value of characters.

ASCII(‘A’) = 65

ASCII(‘B’) = 66

.

.

.

ASCII(‘Z’) = 90

Properties of Hash Functions

• If H(x) = H(y) then x and y might be equal, but if H(x) != H(y) then x and y are not equal. This means that instead of comparing x and y directly, a smarter approach is to first compare their hash values, and only if they match then check explicitly for x and y.

• A hash function must be deterministic, meaning if H(x) = y then H(x) should always produce y as the output.

• It should be uniform to minimize the number of hash collisions, i.e, H(x) = H(y).

We have one more important question to address, What makes a key of type T hashable?

As we discussed in the properties of hash functions, it needs to be deterministic, and to ensure this behavior we must have immutable data type keys for our hash table.

Working of a Hash Table

When we talk of the hash table we expect fast insertion, retrieval, and deletion time for data we have in our hash table. And to our surprise, we can achieve all of it in O(1) time complexity (given it has a uniform hash function) using a hash function as a way to index into a hash table.

Let’s see an example to get better clarity.

Suppose we are storing the marks of students which will be (integer, string) key-value pair. Here the marks (integer) would serve as the key and name (string) as the value.

Hash function we are going to use:

H(x) = x^3 + 9 mod 10

Let’s insert the following key-value pairs and update the changes in our hash table.

(99, “srajan”) , H(x) = 99^3 + 9 mod 10 = 8

(66, “nikhil”) , H(x) = 66^3 + 9 mod 10 = 5

(97, “kamli”) , H(x) = 97^3 + 9 mod 10 = 2

(100, “obaid”) , H(x) = 100^3 + 9 mod 10 = 9

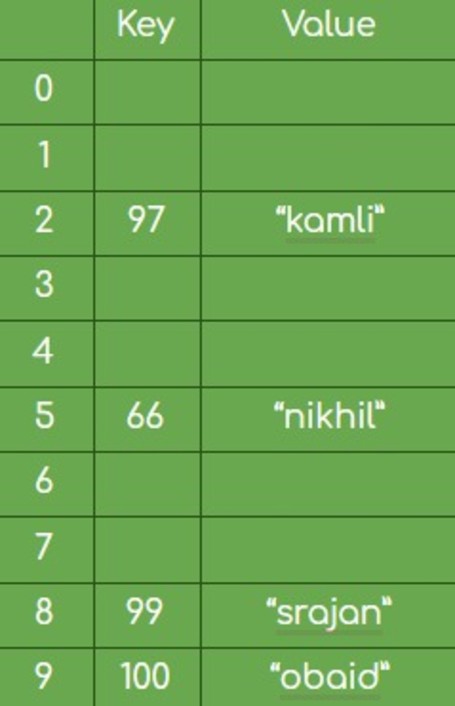
As we have inserted our students into the hash table, to retrieve a student with specific marks we can simply compute the H (marks) value and then lookup the student in the hash table for the corresponding hash value.

Code implementation for our example:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<bits/stdc++.h>

using namespace std;

int hash_function(int x, int hash_table_size) {
  return (x * x * x + 9) % hash_table_size;
}

int main() {
  int n;
  cin >> n;
  int hash_table_size;
  cin >> hash_table_size;

  vector < string > hash_table(hash_table_size);

  int key;
  string value;
  while (n--) {
    cin >> key >> value;

    int hx = hash_function(key, hash_table_size);

    // inserting into hash_table
    hash_table[hx] = value;
  }

  // loopkup for student with r marks
  int r;
  cin >> r;
  int hx = hash_function(r, hash_table_size);
  cout << hash_table[hx] << endl;
}

Input:

1
2
3
4
5
6
7
4
10
99 srajan
66 nikhil
97 kamli
100 obaid
99

Output:

srajan

Now comes the part where we try to minimize our hash collisions. For this we use many hash collision resolution techniques. Two of the most popular are separate chaining and open addressing, which will be discussed in a future article.

Complexity

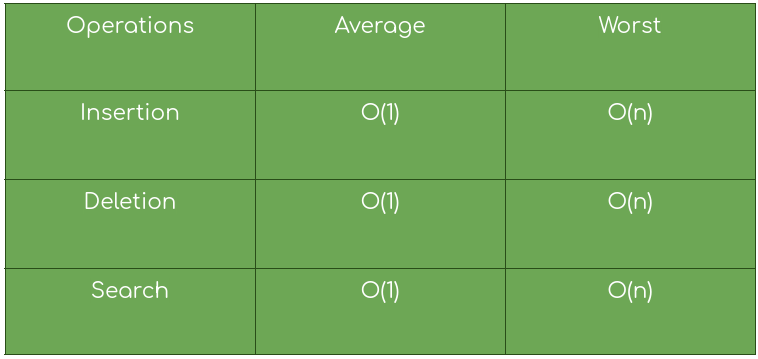
O(1) is possible only in those cases where we have a good uniform hash function.

What is Separate Chaining?

Separate chaining is one of the many hash collision resolution techniques used by maintaining a data structure to hold all the different values which hashed to a particular value.

When there is a hash collision, i.e, when two keys hash to the same value, we need to have some way of handling that within our hash table so its functionality is maintained. Separate chaining maintains an auxiliary data structure to hold all the collisions so we can go back and look up inside that data structure for values of the items we are looking for.

The data structure used to store the items which hashed to a particular value is mainly a linked list but some implementations use different data structures like arrays, binary trees, self-balancing trees, etc.

Linked List Separate Chaining

Insertion:

Suppose we are storing the marks of students which will be (string, integer) key-value pairs. Here the marks (integer) serve as the value and name (string) as the key.
We can use any hash function to compute our hash value, for now we are taking values to make some collisions.

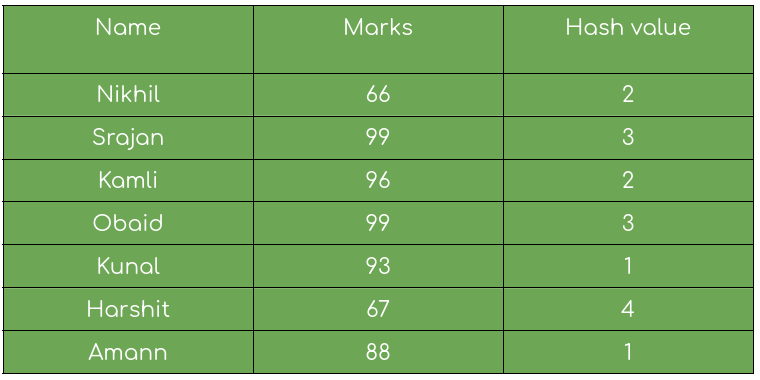
You can see from the table that some students have the same hash value, like Nikhil and Kamli, but their marks are different. In situations like these if we don’t hash right we might mix up the marks.

As we stated above we are going to use a linked list to do separate chaining. We will now insert all the above key-value pairs one by one into our new hash tables via separate chaining.

We insert until we get a collision.

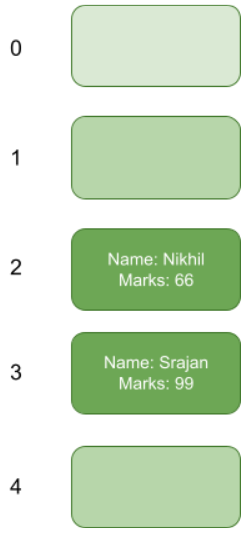
Now we try to insert Kamli who has a hash of 2 but Nikhil is already there. In separate chaining, we just chain along, essentially each position in our hash table is a linked list data structure. So now we scan through the corresponding linked list and see if the key already exists. In our case it is Kamli, if Kamli doesn’t exist we are going to add him at the very end of the chain. We store the key because when there is a hash collision they might have the same marks, so to tell them apart we store their names in the linked list block.

After inserting all our key-pairs:

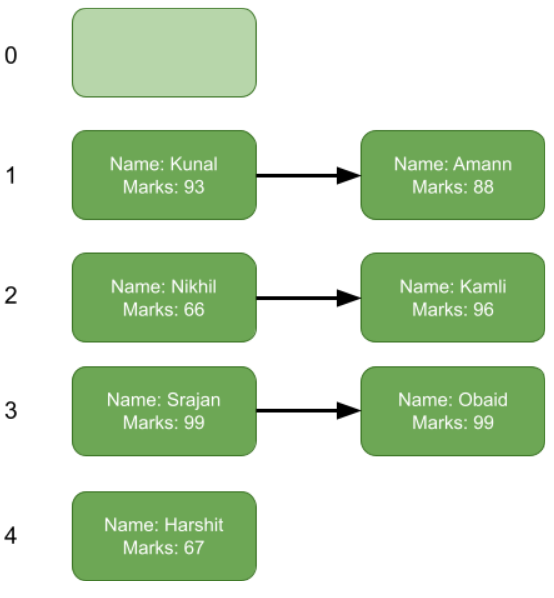
Retrieving:

Now to find the mark of “Amann” we hash “Amann” to obtain the hash value, i.e 1. After this, we search the 1 linked list for “Amann” until we either reach the end or find it.

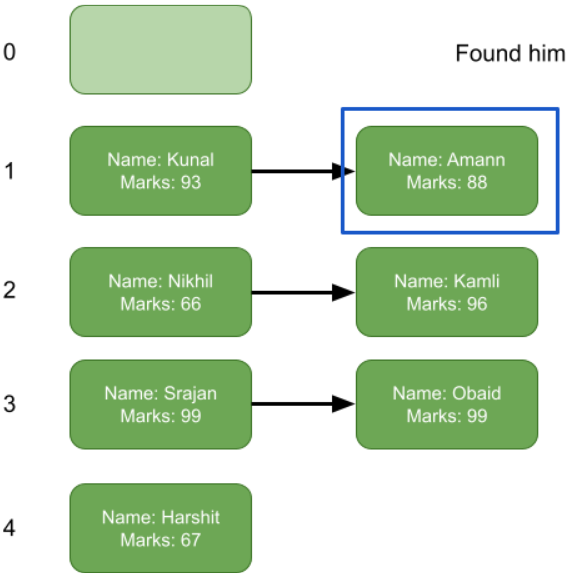
In our case, we can find “Amann” and return his mark, i.e 88.

Code Implementation:

Below is a simpler problem code than what we discussed above, but it serves its purpose.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include<bits/stdc++.h>

using namespace std;

class Hash {
  int HASH_SIZE;
  vector < int > * hash_table;

  public:
    Hash(int V);

  void insertItem(int x);

  int hashFunction(int x) {
    return (x % HASH_SIZE);
  }

  void displayHash();
};

Hash::Hash(int b) {
  this - > HASH_SIZE = b;
  hash_table = new vector < int > [HASH_SIZE];
}

void Hash::insertItem(int key) {
  int index = hashFunction(key);
  hash_table[index].push_back(key);
}

void Hash::displayHash() {
  for (int i = 0; i < HASH_SIZE; i++) {
    cout << i;
    for (auto x: hash_table[i])
      cout << " --> " << x;
    cout << endl;
  }
}

int main() {
  int n;
  cin >> n;

  vector < int > a(n);
  for (int i = 0; i < n; i++) cin >> a[i];

  int hash_size;
  cin >> hash_size;

  Hash h(hash_size);
  for (int i = 0; i < n; i++)
    h.insertItem(a[i]);

  h.displayHash();

  return 0;
}

Input:

1
2
3
8
12 15 66 78 99 36 58 77
7

Output:

1
2
3
4
5
6
7
0-- > 77
1-- > 15-- > 78-- > 99-- > 36
2-- > 58
3-- > 66
4
5-- > 12
6

Note: If your HT gets really big, to maintain your linear time insertion and retrieval you should create a new HT with larger capacity, rehash all the items again, and disperse them throughout the new HT at different locations.