Getting Started with Hash Table Data Structure- Open Addressing and Linear Probing

Check the prequel article Getting Started with Hash Table Data Structure - Introduction.

Why Use Open Addressing?

When we make a hash table (HT) our goal is to construct mapping from keys to values, where the keys must be hashable and we need a hash function to convert those keys to whole numbers. Then we use those hash values to index our key set into an array.

Hash functions aren’t easy to master, so we might not be perfect. Therefore, sometimes two keys x and y (x!=y) might hash to the same value. When this happens we have a hash collision (i.e H(x) = H(y) ). Open addressing is a way to solve this problem.

While open addressing we store the key-value pairs in the table itself, as opposed to a data structure like in separate chaining, which is also a technique for dealing with a hash collision.

To accommodate all the key-value pairs we need a bigger hash table. To calculate the load factor we can use the equation below:

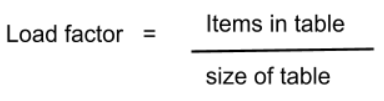
Main Objective of Open Addressing:

When we insert a key-value pair (k,v) into the hash table we hash the key and get an original position to where this key-value pair belongs i.e H(k)

If the corresponding position is already occupied, then we try another position in the hash table by offsetting the current position subject to a probing sequence P(x), repeating until we get an unoccupied slot.

There are number of probing sequences we can use, below are few of them:

Linear probing: P(x) = ax + b where a,b are constants

Quadratic probing: P(x) = ax + bx + c where a,b,c are constants

Double probing: P(k,x) = x*H2(k), where H2(k) is a secondary hash function

Pseudo random number probing: x*RNG(H(k),x), where RNG is a random number generator function seed with H(k)

We will be discussing the above probing techniques briefly in future articles.

Insertion:

For a hash table of size N,

Pseudocode:

1
2
3
4
5
6
7
8
9
x = 1 // incremented each time we fail to hit a free position
keyHash = H(k) mod N
Index = keyHash

While hash_table[index] != null:
  index = (keyHash + P(k, x)) mod N
x = x + 1

hash_table[index] = (k, v)

• First, we calculate the key hash using a hash function H(x),

• Now we change our index until we land on an index where hash_table[index] != null,

• To calculate the next index we add the probing function to the key hash and take the mod again with N and increment the value of x every time by one,

• Then when we find the index store the key-value pair.

Problem With the Above Algorithm:

Randomly selected probing sequences mod N will produce a cycle shorter than the table size N. We might get stuck in an infinite loop if all the positions in the hash table are occupied based on the cycle.

In general, we don’t handle this issue. Instead, we avoid it altogether by restricting our domain of probing functions to those which produce a cycle exactly the length N.

Techniques such as linear probing, quadratic probing, and double hashing are all subject to the issue of causing cycles which is why the probing functions used with these methods are very specific. This is a large topic that will be the focus of our next few articles.

In this article we will cover linear probing and the other two in the next:

What is Linear Probing?

Linear probing (LP) is a probing method which probes according to a linear formula, for example:

P(x) = ax + b where a(!=0), b are constants

But, as we observed earlier, not every LP is viable because they are unable to produce a cycle of size N. We will need to handle this.

Suppose if our linear function is P(X) = 2x, H(k) = 4, and table size is 8, we end up with the following cycle occurring:

H(k) + P(0) mod N = 4  
H(k) + P(1) mod N = 6
H(k) + P(2) mod N = 0
H(k) + P(3) mod N = 2
H(k) + P(4) mod N = 4
H(k) + P(5) mod N = 6
H(k) + P(6) mod N = 0
H(k) + P(7) mod N = 2

The cycle {4,6,0,2} makes it impossible to reach buckets {1,3,5,7}. This would cause an infinite loop if all the buckets {4,6,0,2} are already occupied.

To solve our above problem we should select the value of the constant in P(x) = ax such that it produces a full cycle modulo N. To achieve this a and N should be relatively prime. Two numbers are relatively prime if their greatest common denominator (GCD) is one i.e GCD(a, N) = 1. This helps the probing function P(x) be able to generate a complete cycle and we will always be able to find an empty bucket.

Let’s try one example-

Here we have a hash table of size N = 9. When we try and insert our key-value pairs (ki,vi), our hash table:

Probing function: P(x) = 6x
Fixed table size: N = 9
Max load factor: α = 0.667
Threshold before resize: N * α = 6

In our current example if we calculate the GCD(9,6) it would come out to be 3, not 1, so we will be facing an infinite loop.

Now let’s illustrate our infinite loop.

Insert the following:

(k1,v1) suppose H(k1) = 2
( H(k1) + P(0) ) mod N = ( 2 + 0 ) mod 9 = 2

(k2,v2) suppose H(k2) = 2
( H(k2) + P(0) ) mod N = ( 2 + 0 ) mod 9 = 2 collision
( H(k2) + P(1) ) mod N = ( 2 + 6 ) mod 9 = 8

(k3,v3) suppose H(k3) = 3
( H(k2) + P(0) ) mod N = ( 3 + 0 ) mod 9 = 3

(k2,v4) ( H(k2) + P(0) ) mod N = ( 2 + 0 ) mod 9 = 2
As we can see it has the same key as the second entry.
Here we just update the value for this key.
( H(k2) + P(1) ) mod N = ( 2 + 6 ) mod 9 = 8 Found it.

(k5,v5) suppose H(k5) = 8
( H(k2) + P(0) ) mod N = ( 8 + 0 ) mod 9 = 8 collision
( H(k2) + P(1) ) mod N = ( 8 + 6 ) mod 9 = 5

(k6,v6) suppose H(k6) = 5
( H(k2) + P(0) ) mod N = ( 5 + 0 ) mod 9 = 5 collision
( H(k2) + P(1) ) mod N = ( 5 + 6 ) mod 9 = 2 collision
( H(k2) + P(2) ) mod N = ( 5 + 12 ) mod 9 = 8 collision
( H(k2) + P(3) ) mod N = ( 5 + 18 ) mod 9 = 5 collision (repeat)
Here we have encountered a infinite loop

Below we can see the loop and our insertions:

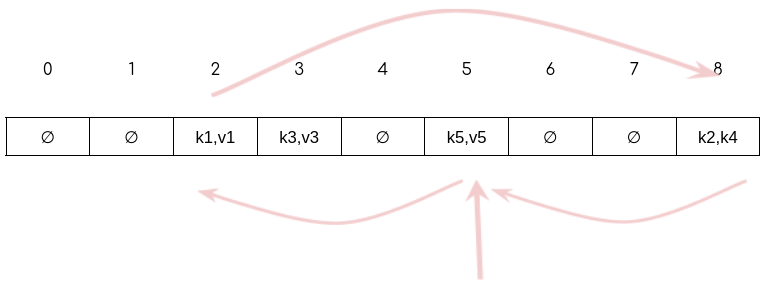
As we knew before, GCD(9,6) = 3, costs us an infinite loop.

GCD(9,1) = 1 GCD(9,4) = 1 GCD(9,7) = 1
GCD(9,2) = 1 GCD(9,5) = 1 GCD(9,8) = 1
GCD(9,3) = 3 GCD(9,6) = 3 GCD(9,9) = 9

Now from the above choices, we are going to use a = 5;

Probing function: P(x) = 5x
Fixed table size: N = 12
Max load factor: α = 0.35
Threshold before resize: N * α = 4

You can go ahead and insert your values into our new table. You won’t get an infinite loop but you will soon reach the threshold, which is 4 in our case. What we do then is grow our table. We can grow it exponentially, such as doubling the size, but the relative prime property must be fulfilled.

Code implementation:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#include <bits/stdc++.h>

using namespace std;

template < typename K, typename V >

  class HashNode {
    public: V value;
    K key;

    HashNode(K key, V value) {
      this - > value = value;
      this - > key = key;
    }
  };

template < typename K, typename V >

  class HashMap {

    HashNode < K, V > ** hash_table;
    int capacity;

    int size;

    HashNode < K, V > * temp;

    public:
      HashMap() {

        capacity = 20;
        size = 0;
        hash_table = new HashNode < K, V > * [capacity];

        for (int i = 0; i < capacity; i++)
          hash_table[i] = NULL;

        temp = new HashNode < K, V > (-1, -1);
      }

    int hashCode(K key) {
      return key % capacity;
    }

    void insertNode(K key, V value) {
      HashNode < K, V > * temp = new HashNode < K, V > (key, value);

      int hashIndex = hashCode(key);

      while (hash_table[hashIndex] != NULL &&
        hash_table[hashIndex] - > key != key &&
        hash_table[hashIndex] - > key != -1) {
        hashIndex++;
        hashIndex %= capacity;
      }

      if (hash_table[hashIndex] == NULL ||
        hash_table[hashIndex] - > key == -1)
        size++;
      hash_table[hashIndex] = temp;
    }

    V get(int key) {

      int hashIndex = hashCode(key);
      int counter = 0;

      while (hash_table[hashIndex] != NULL) {

        if (counter++ > capacity)
          return NULL;

        if (hash_table[hashIndex] - > key == key)
          return hash_table[hashIndex] - > value;
        hashIndex++;
        hashIndex %= capacity;
      }

      return NULL;
    }

  };

int main() {
  HashMap < int, int > * h = new HashMap < int, int > ;

  int n;
  cin >> n;
  int k, v;
  for (int i = 0; i < n; i++) {
    cin >> k >> v;
    h - > insertNode(k, v);
  }
  cout << h - > get(2);

  return 0;
}

Input:

1
2
3
4
3
1 1
2 2
2 3

Output:

3

Note:
Open addressing is much more sensitive to hashing and probing functions used. But that is not the case while using separate chaining as in a collision resolution method.