Kadane's Algorithms

Say we are given an array containing positive and negative numbers and we need to find the sum of the largest contiguous subarray from the given array. We can find the largest sum with the divide and conquer approach or brute force with O(NLogN) and O(N*N). But, with the help of Kadane’s algorithm we can reduce the complexity of finding the largest subarray sum to O(N).

pseudo Code for Kadane’s Algorithm

1
2
3
4
5
6
7
8
9
10
11
12
Declaration
Var Max_So_Far = Integer.MIN_VALUE
Var Max_End_Here = 0
Iterating whole Array(i = 0..N - 1)
step 1 Max_End_Here = Max_End_Here + Array[i]
step 2
if (Max_So_Far < Max_End_Here)
  then Max_So_Far = Max_End_Here
step 3
if (Max_End_Here < 0)
  then Max_End_Here = 0
return Max_So_Far

Let’s understand the algorithm with the help of an example.
Suppose we are given array below:

In it, the subarray with the largest contiguous sum is " 4, -1, 2, 5", which is starting from the second index to the fifth index. Now let us figure out the largest sum of the given array with the help of Kadane’s algorithm in O(N) complexity.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
Max_End_Here = MEH
Max_So_Far = MSF
Iteration 1: i = 0, MEH = 0, MSF = Integer.MIN_VALUE, arr[0] = -2
step1 MEH = 0 + (-2), so MEH = -2
step2(Integer.MIN_VALUE < -2) -- > True
MSF = -2
step3(-2 < 0) -- > True
MEH = 0
Result: MEH = 0, MSF = -2
Iteration 2: i = 1, MEH = 0, MSF = -2, arr[1] = -3
step1 MEH = 0 + (-3), so MEH = -3
step2(-2 < -3) -- > False

step3(-3 < 0) -- > True
MEH = 0
Result: MEH = 0, MSF = -2

Iteration 3: i = 2, MEH = 0, MSF = -2, arr[2] = 4
step1 MEH = 0 + (4), so MEH = 4
step2(-2 < 4) -- > True
MSF = 4
step3(4 < 0) -- > False
MEH = 0 // will not execute
Result: MEH = 4, MSF = 4

Iteration 4: i = 3, MEH = 4, MSF = 4, arr[3] = -1
step1 MEH = 4 - 1, so MEH = 3
step2(4 < 3) -- > False
MSF = 4 // no execute
step3(3 < 0) -- > False
MEH = 0 // will not execute
Result: MEH = 3, MSF = 4

Iteration 5: i = 4, MEH = 3, MSF = 4, arr[4] = 2
step1 MEH = 3 + 2, so MEH = 5
step2(4 < 5) -- > True
MSF = 5
step3(5 < 0) -- > False
MEH = 0 // will not execute
Result: MEH = 5, MSF = 5

Iteration 6: i = 5, MEH = 5, MSF = 5, arr[5] = 5
step1 MEH = 5 + 5, so MEH = 10
step2(5 < 10) -- > True
MSF = 10
step3(10 < 0) -- > False
MEH = 0 // will not execute
Result: MEH = 10, MSF = 10

Iteration 6: i = 6, MEH = 10, MSF = 10, arr[6] = -3
step1 MEH = 10 - 3, so MEH = 7
step2(10 < 7) -- > False
MSF = 7 // Not Execute
step3(7 < 0) -- > False
MEH = 0 // will not execute
Result: MEH = 7, MSF = 10

Iteration ended:

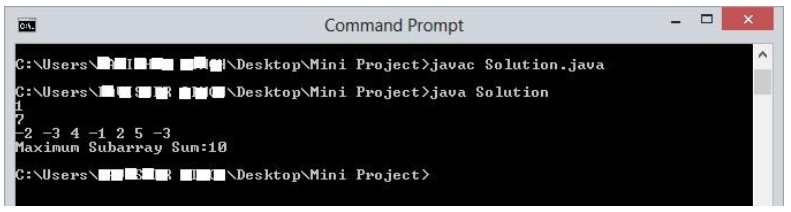
Now we have come out of the loop and the Maximum_So_Far value, which is 10, will be returned.

Complexity Analysis

We have only traversed the array once so the time complexity for Kadane’s Algorithm is O(N). We are using only two variables and no other extra space or array is created, hence the space complexity is O(1).

Java Implementation of Kadane’s Algorithm

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import java.util.*;
import java.lang.*;
import java.io.*;

class Solution {
  public static void main(String[] args) throws IOException {
    BufferedReader bf = newBufferedReader(new InputStreamReader(System.in));

    int test = Integer.parseInt(bf.readLine());

    while (test > 0) {
      test--;
      int N = Integer.parseInt(bf.readLine());

      String line = bf.readLine();
      String str[] = line.trim()
        .split("\\s+");

      int arr[] = new int[N];

      for (int i = 0; i < N; i++) {
        arr[i] = Integer.parseInt(str[i]);

      }

      int max_so_far = Integer.MIN_VALUE;
      int max_end_here = 0;

      for (int i = 0; i < N; i++) {
        max_end_here += arr[i];

        if (max_so_far < max_end_here)
          max_so_far = max_end_here;

        if (max_end_here < 0)
          max_end_here = 0;
      }

      System.out.println("Maximum Subarray Sum:" + max_so_far);
    } // while test case ends

  }
}

Code output: