Huffman Coding and Decoding Algorithm

Huffman coding is an algorithm for compressing data with the aim of reducing its size without losing any of the details. This algorithm was developed by David Huffman.

Huffman coding is typically useful for the case where data that we want to compress has frequently occurring characters in it.

How it works

Let assume the string data given below is the data we want to compress -

The length of the above string is 15 characters and each character occupies a space of 8 bits. Therefore, a total of 120 bits ( 8 bits x 15 characters ) is required to send this string over a network. We can reduce the size of the string to a smaller extent using Huffman Coding Algorithm.

In this algorithm first we create a tree using the frequencies of characters and then assign a code to each character. The same resulting tree is used for decoding once encoding is done.

Using the concept of prefix code, this algorithm avoids any ambiguity within the decoding process, i.e. a code assigned to any character shouldn’t be present within the prefix of the opposite code.

Steps to Huffman Coding

1. First, we calculate the count of occurrences of each character in the string.

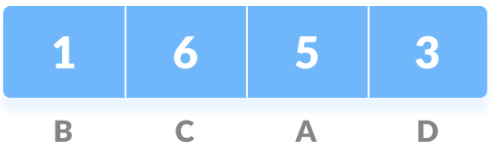
2. Then we sort the characters in the above string in increasing order of the count of occurrence. Here we use PriorityQueue to store.

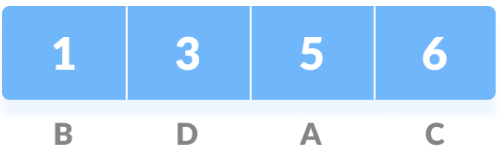
3. Now we mark every unique character as a Leaf Node.

4. Let’s create an empty node n. Add characters having the lowest count of occurrence as the left child of n and second minimum count of occurrence as the right child of n, then assign the sum of the above two minimum frequencies to n.

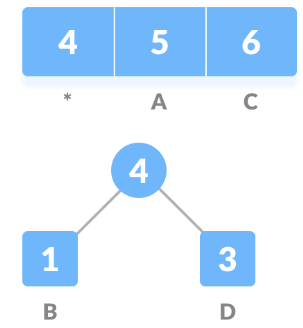
5. Now remove these two minimum frequencies from Queue and append the sum into the list of frequencies.

6. Add node n into the tree.

7. Just like we did for B and D, we repeat the same steps from 3 to 5 for the rest of the characters ( A and C ). For A -

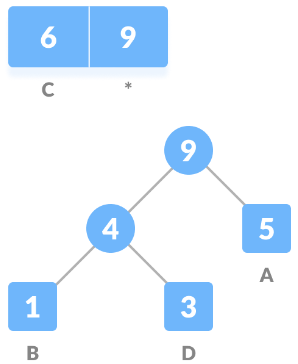
Repeat for C -

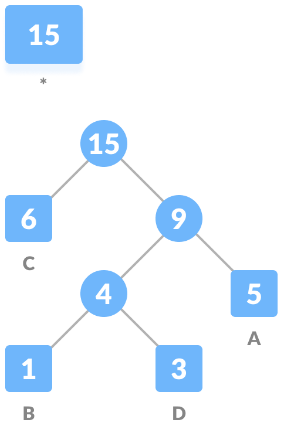
8. We got our resulting tree, now we assign 0 to the left edge and 1 to the right edge of every non-leaf node.

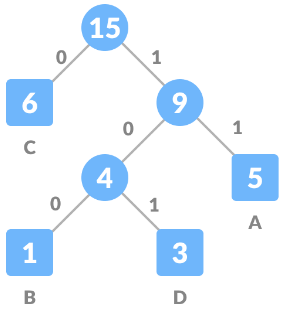
9. Now for generating codes of each character we traverse towards each leaf node representing some character from the root node and form code of it.

All the data we gathered until now is given below in tabular form -

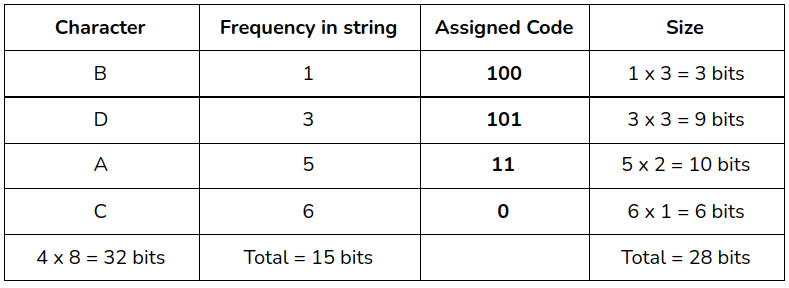
Before compressing the total size of the string was 120 bits. After compression that size was reduced to 75 bits (28 bits + 15 bits + 32 bits).

Steps to Huffman Decoding

To decode any code, we take the code and traverse it in the tree from the root node to the leaf node, each code will make us reach a unique character.

Let assume code 101 needs to be decoded, for this we will traverse from the root as given below -

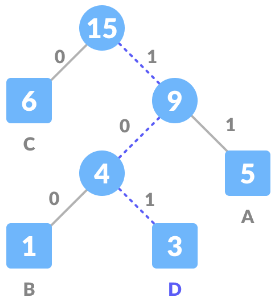
As per the Huffman encoding algorithm, for every 1 we traverse towards the right child and for 0 we traverse towards the left one, if we follow this and traverse, we will reach leaf node 3 which represents D. Therefore, 101 is decoded to D.

Algorithm

1
2
3
4
5
6
7
8
9
10
11
12
13
14
create and initialize a PriorityQueue Queue consisting of each
unique character.
sort in ascending order of their frequencies.
for all the unique characters:
  create a new_node
get minimum_value from Queue and set it to left child of
  new_node
get minimum_value from Queue and set it to right child of
  new_node
calculate the sum of these two minimum values as
sum_of_two_minimum
assign sum_of_two_minimum to the value of new_node
insert new_node into the tree
return root_node

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
import java.util.PriorityQueue;
import java.util.Comparator;

class HuffmanNode {
  int data;
  char charData;
  HuffmanNode left;
  HuffmanNode right;
}

// Comparing two nodes
class ImplementComparator implements Comparator < HuffmanNode > {
  public int compare(HuffmanNode node1, HuffmanNode node2) {
    return node1.data - node2.data;
  }
}

// Huffman algorithm
public class Huffman {

  public static boolean isLetter(char c) {
    return Character.isLetter(c);
  }

  public static void printCode(HuffmanNode node, String s) {
    if (node.left == null && node.right == null && isLetter(node.charData)) {
      System.out.println(node.charData + "   |  " + s);
      return;
    }

    printCode(node.left, s + "0");
    printCode(node.right, s + "1");
  }

  public static void main(String[] args) {

    int n = 4;

    char[] charArray = {
      'B',
      'C',
      'A',
      'D'
    };
    int[] char_frequency = {
      1,
      6,
      5,
      3
    };

    PriorityQueue < HuffmanNode > queue = new PriorityQueue < HuffmanNode > (n, new ImplementComparator());

    for (int in = 0; in < n; in ++) {
      HuffmanNode node = new HuffmanNode();

      node.charData = charArray[in];
      node.data = char_frequency[in];

      node.left = null;
      node.right = null;

      queue.add(node);
    }

    HuffmanNode root = null;

    while (queue.size() > 1) {

      HuffmanNode min_freq_node = queue.poll();
      HuffmanNode second_min_freq_node = queue.poll();

      HuffmanNode f_node = new HuffmanNode();

      f_node.data = min_freq_node.data + second_min_freq_node.data;
      f_node.charData = '-';
      f_node.left = min_freq_node;
      f_node.right = second_min_freq_node;

      root = f_node;

      queue.add(f_node);
    }
    printCode(root, "");
  }
}

Complexity

• O(nlogn) complexity for encoding each character based on their frequency.

• Getting minimum frequency from queue occurred 2*(n-1)times and its complexity is O(nlogn), so overall complexity is O(nlogn).